手元に1969年の日本書院の教科書がある. 数学IIBと数学III では区間の分割が等分か任意の分割かが違うのだが, 本質的に同じなので,ここでは数学III の定義を紹介しよう. 次のように書かれている.
関数![]() は閉区間
は閉区間![]() で連続とする.
で連続とする.
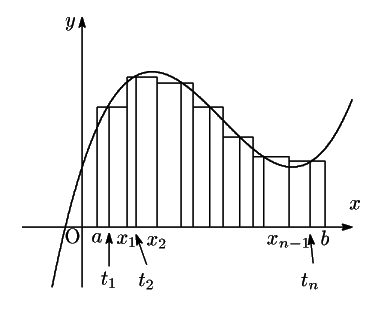
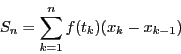
すべての小区間の長さが,いずれも0に近づくように![]() を限りなく大きくするとき,
を限りなく大きくするとき,
![]() の点のとり方にかかわらず,
和
の点のとり方にかかわらず,
和![]() は一定の極限値に近づくことが知られている.
は一定の極限値に近づくことが知られている.
この極限値を,関数![]() の区間
の区間![]() における定積分といい
における定積分といい
史織 区分求積法に出てくる和の極限値が定積分の定義なのですね. つまり,現在の教科書で区分求積法といわれる(3)は, じつは定積分の定義なのですね.
南海 そうなのだ,1969年にはこのように書かれていた. 連続なら収束することは,証明はないが正しく指摘されている. さらに,1984年に初版が出た『問題新集 微分・積分基本500選』(科学新興社)では, まとめに次のように書かれている.
![]() とする.
とする.![]() を区間
を区間![]() で定義された関数とする.分割
で定義された関数とする.分割
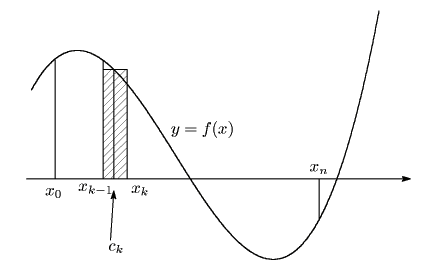
極限値
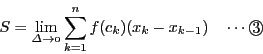
南海
これが正確な定積分の定義だ.
この和
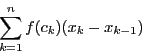
この定義では「![]() が存在するとき」と書かれているがそれは
が存在するとき」と書かれているがそれは
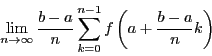
関数![]() が区間
が区間![]() で連続ならば,
で連続ならば,![]() の点
の点![]() に関して,
に関して,![]() の関数
の関数
史織 ![]() の極限が
の極限が![]() が連続なら存在するのですか.
が連続なら存在するのですか.
南海
そうだ.理論的にはそこが肝心なところなのだ.その証明自体は高校範囲を超える.
大切なことは,積分は![]() の和の極限として定まり,
の和の極限として定まり,
![]() の所では
の所では![]() と
と![]() 軸で囲まれた図形の面積だ,ということだ.
軸で囲まれた図形の面積だ,ということだ.
史織
そうすると,この定積分の定義と面積の関係は,
![]() のグラフと
のグラフと![]() 軸で囲まれた図形の
軸で囲まれた図形の![]() 軸の上にある部分の面積を
軸の上にある部分の面積を![]() で,
下にある部分の面積を
で,
下にある部分の面積を![]() でとり加えたものになるのですね.
でとり加えたものになるのですね.
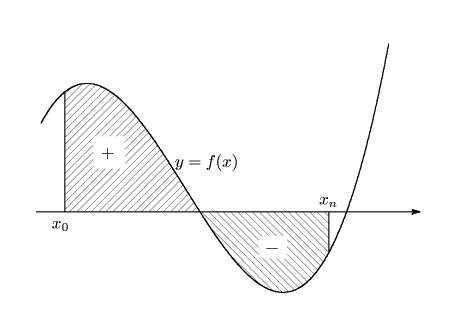
南海 その通りだといいたいのだが,しかしここには一つの問題が潜んである. それは何かというと,そもそも面積とは何か,という問題だ.
史織 当然のように面積を全体に考えてきましたが,複雑な関数で面積とは何か. たしかに,この面積という数値をどのように求めるのか. これ自体が定義されていない,ということですね.
南海
実は,![]() のとき,定積分
のとき,定積分
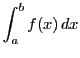 の値をもって,
の値をもって,
![]() と
と![]() 軸と
軸と![]() で囲まれた図形の面積と定義する.
で囲まれた図形の面積と定義する.
史織 そうすると,いま言った,定積分と面積の関係は定義そのもになる.
南海 この観点で最初から書いたのが,『解析基礎』だ.高校生が読むのも不可能ではない.