南海
ここで二つの集合![]() と
と![]() に対し,集合
に対し,集合![]() から集合
から集合![]() への写像の集合をべき集合といい
への写像の集合をべき集合といい
これは次の例で考えれば,自然な記号だ.![]() で
で
![]() なら,
なら,![]() から
から![]() への写像は0と1の行き先を決めれば決まるので,その組合せだけあり,個数は
への写像は0と1の行き先を決めれば決まるので,その組合せだけあり,個数は![]() 個ある.
個ある.
有限集合の場合,![]() から
から![]() への写像の集合は,集合
への写像の集合は,集合![]() を集合
を集合![]() の分だけ組合わせただけあり,その個数は
の分だけ組合わせただけあり,その個数は
![]() 個ある.
個ある.
これをもとに,べき集合を上のように定義した.
したがって,実数の実数べき集合![]() とは,実数から実数への写像の集合である.
とは,実数から実数への写像の集合である.
証明
実数![]() と定数写像
と定数写像![]() を対応させることで
を対応させることで![]() は
は![]() の部分集合と一対一の対応がつけられる.したがって
の部分集合と一対一の対応がつけられる.したがって
次に![]() と
と![]() の間に一対一写像は存在しないことを示す.
の間に一対一写像は存在しないことを示す.
集合![]() と
と![]() の間に一対一対応が存在すると仮定する.
の間に一対一対応が存在すると仮定する.
この一対一対応で実数![]() に対応する写像を
に対応する写像を![]() とおく.ここで
とおく.ここで![]() から
から![]() への写像,つまり
への写像,つまり![]() の要素
の要素![]() を次のように定める.
を次のように定める.
ゆえに集合![]() と
と![]() の間に一対一対応は存在しない.□
の間に一対一対応は存在しない.□
拓生 実数なので対角線に並べるということはできないが,しかし,実数と一対一対応があるとして,自己言及するところで矛盾した写像を作るということは,定理1 の証明の別表現と同じです.
南海 その通りである.
集合![]() に対し,その部分集合の集合(空集合と
に対し,その部分集合の集合(空集合と![]() 自身を含む)を
自身を含む)を![]() と書こう.これは
と書こう.これは![]() から集合
から集合![]() への写像の集合の記号
への写像の集合の記号![]() から来ている.
から来ている.
集合![]() に対し,その部分集合の集合と,
に対し,その部分集合の集合と,![]() から集合
から集合![]() への写像の集合との間に一対一の対応が存在する.
への写像の集合との間に一対一の対応が存在する.
つまり,集合![]() の部分集合
の部分集合![]() が一つ与えられると,
が一つ与えられると,![]() から集合
から集合![]() への写像
への写像![]() が
が
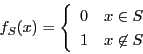
![]() が
が![]() 個の要素からなる有限集合の場合,部分集合は各要素を含むか含まないかで決まるので,部分集合の個数は
個の要素からなる有限集合の場合,部分集合は各要素を含むか含まないかで決まるので,部分集合の個数は![]() 個ある.つまり有限集合の場合は
個ある.つまり有限集合の場合は
だから,![]() から集合
から集合![]() への写像の集合を,
への写像の集合を,![]() のべき集合といい,
のべき集合といい,![]() と記すことにする.
と記すことにする.
証明
![]() の要素
の要素![]() に対して,
に対して,![]() から集合
から集合![]() への写像
への写像![]() を
を
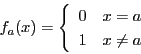
集合![]() と
と![]() の間に一対一対応が存在すると仮定する.
の間に一対一対応が存在すると仮定する.
この一対一対応で集合![]() の要素
の要素![]() に対応する
に対応する![]() の部分集合を
の部分集合を![]() とする.
とする.
![]() の部分集合
の部分集合![]() を次のように定める.
を次のように定める.
![]() もまた
もまた![]() の部分集合なので,
の部分集合なので,![]() のある要素
のある要素![]() と対応している.つまり
と対応している.つまり
しかしこのとき,もし![]() なら
なら![]() の定義から
の定義から
![]() なので矛盾,
もし
なので矛盾,
もし![]() ,つまり
,つまり![]() が
が![]() の補集合の要素なら
の補集合の要素なら![]() の定義から
の定義から![]() なので矛盾,
なので矛盾,
いずれも矛盾となる.ゆえに集合![]() と
と![]() の間に一対一対応は存在しない.つまり
の間に一対一対応は存在しない.つまり
南海
![]() が
が![]() つまり自然数の集合のとき
つまり自然数の集合のとき
拓生
定理1から
![]() ですが,
ですが,![]() と
と![]() はどちらが大きいのだろう.
はどちらが大きいのだろう.
南海
拓生
![]() とは自然数から
とは自然数から![]() への写像の集合です.これはつまり
への写像の集合です.これはつまり![]() が0か1の値をとるような写像なので,一つの写像
が0か1の値をとるような写像なので,一つの写像![]() に対して
に対して
あっ.これを
これで![]() と区間
と区間![]() の間の一対一対応ができる.
の間の一対一対応ができる.
南海 その通りである.
カントールは,数直線![]() と平面
と平面![]() の間に一対一対応があるかという問題にも取り組んだ.おそらくないだろうと見込みを付け,それを証明しようと3年にわたって研究を続ける.その結果,彼が得た結論は一対一対応が存在するというものであった.彼はその証明を伝えたデーデキントへのドイツ語で書かれた書簡の中で、有名な
の間に一対一対応があるかという問題にも取り組んだ.おそらくないだろうと見込みを付け,それを証明しようと3年にわたって研究を続ける.その結果,彼が得た結論は一対一対応が存在するというものであった.彼はその証明を伝えたデーデキントへのドイツ語で書かれた書簡の中で、有名な
”Je le vois, mais je ne le crois pas”「私は見る、しかし信じられない」
という言葉をそこだけフランス語で書き残している.
数直線全体と,平面全体の一対一対応は演習とする.ここでは次のことを示そう.
証明
区間![]() の数を無限小数で表し
の数を無限小数で表し
これを偶数番目と奇数番目に分けて領域![]() の点
の点
これは明らかに区間![]() と領域
と領域![]() のあいだの一対一対応である.□
のあいだの一対一対応である.□
南海 ここで大問題が生まれる.
濃度と濃度
に対し,
となる濃度は存在するか.
拓生
これまで出てきた,![]() より大きい濃度は,すべて
より大きい濃度は,すべて![]() かまたはそれより大きいものばかりでした.あいだの濃度があるか,ということですね.
かまたはそれより大きいものばかりでした.あいだの濃度があるか,ということですね.
南海
カントールは,![]() の次の濃度は
の次の濃度は![]() であって,あいだの濃度はないと予想した.これを連続体仮説という.
であって,あいだの濃度はないと予想した.これを連続体仮説という.
さらにこれを一般化する.
無限集合に対して,
となる集合これは一般連続体仮説と呼ばれている.集合論の深化はこのような大問題を提起した.は存在しない.
それだけではない.次にもう一つの問題が生まれた.「クレタ人の逆理」のような逆理が生じることが発見されたのだ.それがラッセルの逆理といわれる集合論の逆理だ.集合論を土台に数学を考えていくことが20世紀初頭には一般的になっていた. 集合論はそれ自体数学的対象であるが,同時にあらゆる分野で,集合論的に考え,集合を用いて定義し,また証明するようになってきていた.
そこに逆理が発見された.これは数学の危機である!
後半はここから入り,さまざまの対角線論法がゲーデルの対角線論法に流れ込み, そこから新しい世界が開かれていくことを学ぼう.