南海 ゲーデルの仕事の意味を知るためには,もう少し19世紀末の数学に現れた,数学の基礎に関する諸問題を知らねばならない.これを対角線論法という視点で見ていこう.
集合論におけるカントールの対角線論法と,そのひろがりを見てみよう.
『数学対話』−「高校数学の土台」−「実数とは何か」で,有理数の集合は自然数の集合と一対一の対応を作ることができるが,実数の集合には自然数との一対一対応が存在しないことを示した.これは偉大な発見だった.無限といっても同じではなく,段階があることをはじめて見いだした.
ここで「実数の集合には自然数との一対一対応が存在しない」を改めて考えよう.二つの集合![]() と
と![]() の間に一対一対応が存在するとき,二つの集合の濃度が等しいといい,
の間に一対一対応が存在するとき,二つの集合の濃度が等しいといい,![]() と書く.有限集合の場合は
と書く.有限集合の場合は![]() は集合
は集合![]() の要素の個数そのものとする.
の要素の個数そのものとする.
集合![]() が集合
が集合![]() のなかに埋め込める,つまり
のなかに埋め込める,つまり![]() の部分集合との間に一対一対応が存在するとき,濃度の関係は
の部分集合との間に一対一対応が存在するとき,濃度の関係は![]() であると書く.
であると書く.![]() ではあるが,
ではあるが,![]() と
と![]() の間の一対一対応は存在しないときは
の間の一対一対応は存在しないときは![]() と書く.
と書く.
これで濃度の大小,相等は定義された.
拓生 まってください.「濃度の大小」は確かに定義されましたが,「濃度」そのものは定義されていません.
南海 確かに.濃度そのものを定義してはいない.濃度を定義するためには,公理的な集合論の準備 や,選択公理などに関する理解が必要である.ここでは,一対一対応がつく集合は,何かが同じであると考え,その同じことにつけられた名前が「濃度」であるとした.
拓生 問題はあるが,いまそれを解決することはできない,ということですね.また勉強してみます.
南海
そういうことにしよう.さて,
自然数の集合と一対一の対応が存在する集合の濃度は,自然数の集合の濃度と等しいわけであるが,この濃度を![]() と書き「アレフ0」と読む.
と書き「アレフ0」と読む.
![]() は,英語の
は,英語の![]() に相当するヘブライ語の文字である.濃度が
に相当するヘブライ語の文字である.濃度が![]() である集合は可付番である,あるいは可算無限であるという.それに対して実数の集合の濃度を
である集合は可付番である,あるいは可算無限であるという.それに対して実数の集合の濃度を![]() と書く.
と書く.
カントールが最初に発見した集合論の定理が,次の定理である.この定理は,実数の集合の濃度は自然数の濃度より大きい,つまり実数の集合は可付番ではないことを意味する.カントールは1874年にはこれを発見していたが,1891年に次の証明のような対角線論法でこれを証明した.
証明
区間 ![]() ,つまり
,つまり![]() を満たす実数の集合を考える.
を満たす実数の集合を考える.
自然数![]() に対して,
に対して,
![$\dfrac{1}{n}\in (0,\ 1]$](images/img32.gif) であるから,自然数から
であるから,自然数から![]() への埋め込みが存在する.よって
への埋め込みが存在する.よって
等号が成立しないことを背理法で証明する.
等号が成立するとする.つまり![]() を満たす実数の集合が可付番であると仮定する.
いいかえると,
を満たす実数の集合が可付番であると仮定する.
いいかえると,![]() を満たす実数全体に番号を付けて次のようにできるとする.
を満たす実数全体に番号を付けて次のようにできるとする.
ここで,
![]() のように途中から後はすべて0が並ぶものを有限小数ということにし,
のように途中から後はすべて0が並ぶものを有限小数ということにし,
![]() のように途中から0になることはないものを無限小数ということにする.
のように途中から0になることはないものを無限小数ということにする.
すると有限小数は
![]() を満たす実数の集合が自然数と一対一に対応すると仮定したので,対応する自然数の順に,
を満たす実数の集合が自然数と一対一に対応すると仮定したので,対応する自然数の順に,![]() にある実数を並べる.それを
にある実数を並べる.それを
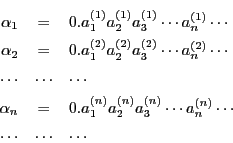
この対角線に並んでいる数![]() に対して,数列
に対して,数列![]() を次のように定める.
を次のように定める.
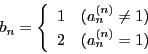
しかし ![]() はどの
はどの ![]() とも一致しない.なぜなら
とも一致しない.なぜなら ![]() と
と ![]() は第
は第 ![]() 位が必ず異なるからである.これは
位が必ず異なるからである.これは
![]() が
が![]() を満たす実数の全体という仮定と矛盾した.
を満たす実数の全体という仮定と矛盾した.
この矛盾は,集合![]() と自然数の集合との間に一対一対応が存在するかぎり起こる.
と自然数の集合との間に一対一対応が存在するかぎり起こる.
よって![]() を満たす実数の集合は可付番でないことが示された.したがって
を満たす実数の集合は可付番でないことが示された.したがって
南海 この背理法を「カントールの対角線論法」という.
さらに次のことが成り立つ.
拓生
つまり,区間![]() と実数全体とのあいだに一対一対応が存在するということですね.
と実数全体とのあいだに一対一対応が存在するということですね.
南海 次のように一対一対応を構成すればよい.
証明
区間![]() を区間の列
を区間の列
区間
![$\left(0,\ \dfrac{1}{2} \right]$](images/img58.gif) は区間
は区間![]() と一対一対応をつけ,
と一対一対応をつけ,
![]() に対しては,
に対しては,
![]() なら区間
なら区間
![$\left(\dfrac{2^n-1}{2^n},\ \dfrac{2^{n+1}-1}{2^{n+1}} \right]$](images/img61.gif) と区間
と区間![]() に一対一対応をつけ,
に一対一対応をつけ,
![]() なら区間
なら区間
![$\left(\dfrac{2^n-1}{2^n},\ \dfrac{2^{n+1}-1}{2^{n+1}} \right]$](images/img61.gif) と区間
と区間![]() に一対一対応をつけることができる.
に一対一対応をつけることができる.
こうして区間![]() と実数の間の一対一対応ができる.□
と実数の間の一対一対応ができる.□
拓生 0と1の間に,すべての有理数より多くの実数があるのは不思議でもあります.
南海 よくたいへん多いことを,「ガンジス川の砂より多い」等というが,それでも,ガンジス川の砂の数は有限だ.
人類が地球上に現れ,言葉を覚えて以来,これまでに生きてきたすべての人間が発した単語の総数,といっても有限だ.
拓生 確かに.地上のすべての人間の細胞の総数,も有限です.それより0と1の間の実数の濃度の方が大きい!
南海
対角線論法は次のように書くこともできる.
定理1の証明の別表現
区間 ![]() の実数
の実数![]() を一つとる.
を一つとる.![]() は十進小数で
は十進小数で
このとき![]() を
を![]() のように関数形で書くと,
のように関数形で書くと,![]() は自然数の集合
は自然数の集合![]() から,
から,![]() と0の集合
と0の集合![]() への写像になっている.
への写像になっている.![]() によって,自然数
によって,自然数![]() に対し
に対し![]() の小数第
の小数第![]() 位の数を対応させる関数が得られる.
位の数を対応させる関数が得られる.
区間 ![]() の実数をひとつとれば,
の実数をひとつとれば,![]() から
から![]() への写像
への写像![]() で恒等的に0ではないものがひとつ定まる.逆に,
で恒等的に0ではないものがひとつ定まる.逆に,![]() から
から![]() への恒等的に0ではない写像
への恒等的に0ではない写像![]() があると,それによって区間
があると,それによって区間 ![]() の実数
の実数![]() がひとつ定まる.
つまり
がひとつ定まる.
つまり
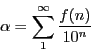
この対応によって,集合![]() と自然数から自然数への写像の集合の間に一対一対応ができる.この対応で二つの集合を同じものとみる.
と自然数から自然数への写像の集合の間に一対一対応ができる.この対応で二つの集合を同じものとみる.
恒等的に0な写像を数0に対応させて
さて,集合
![]() と自然数の間に一対一対応が存在すると仮定する.
と自然数の間に一対一対応が存在すると仮定する.
この一対一対応で自然数![]() に対応する写像を
に対応する写像を![]() とおく.
これを用いて
とおく.
これを用いて![]() から
から![]() への写像
への写像![]() を次のように定める.
を次のように定める.
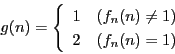
![]() もまた
もまた![]() から
から![]() への写像であるから,ある自然数と対応している.
それを
への写像であるから,ある自然数と対応している.
それを![]() とする.つまり
とする.つまり
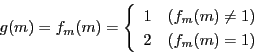
ゆえに集合
![]() と自然数の間に一対一対応は存在しない.□
と自然数の間に一対一対応は存在しない.□
拓生
![]() 番目の関数に
番目の関数に![]() を代入して,その値を否定した値で新たな関数を作る,自己言及関数から新たな関数を作るのですね.
を代入して,その値を否定した値で新たな関数を作る,自己言及関数から新たな関数を作るのですね.
南海 そういうことだ.これは,先の証明を関数形でいいかえただけだが,関数の形で表すことで,次のように発展していく.