


次: SL(2)の分解
上: 方程式の不変式
前: 方程式の不変式
耕介
そこで質問です.
2つの不変式を知りました.
- 第1.
- 方程式の
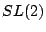 の変換に関して判別式や終結式は不変である.
の変換に関して判別式や終結式は不変である.
- 第2.
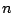 変数の変数の置きかえによる不変式,つまり対称式.
変数の変数の置きかえによる不変式,つまり対称式.
ところが,対称式の場合,
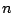 変数の対称式は無数にある.
変数の対称式は無数にある.
- しかし,
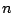 個の基本対称式によって書き表すことが出来る.
個の基本対称式によって書き表すことが出来る.
が成り立ちます.すると,方程式の変換の場合も
- 不変式は判別式以外にもあるのか.
- それらはいくつかの不変式で書き表すことが出来るのか.
という問題が生まれます.
南海
そうだ.
問題を自分の方から設定するのは大変いいことだ.
高校範囲で出来ることにはかぎりがあるが,
2次方程式の変換による不変式が,
判別式,またはそのべきしかないことを確認していこう.
これからは不変式論の伝統にしたがって,
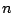 次の方程式を
次の方程式を
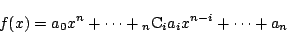 |
(5) |
とおこう.
耕介
2次方程式の場合は
で考えるのですね.すると,変換式(1)も変わります.
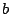 と
と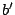 を
を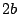 と
と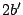 に置きかえるので
に置きかえるので
とおくと
となり第2式が
となります.行列で書くと
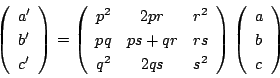 |
(6) |
となります.
そして判別式は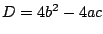 なので,
なので,
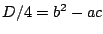 について考えればいいです.
について考えればいいです.
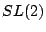 の要素
の要素
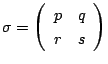 に対して,2次方程式の係数の変換(6)が定まる.
この変換で不変なものが
に対して,2次方程式の係数の変換(6)が定まる.
この変換で不変なものが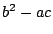 のみであることを示したい,
ということですね.
のみであることを示したい,
ということですね.
Aozora Gakuen
![]() 次の方程式を
次の方程式を

![]() の要素
の要素
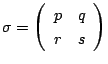 に対して,2次方程式の係数の変換(6)が定まる.
この変換で不変なものが
に対して,2次方程式の係数の変換(6)が定まる.
この変換で不変なものが![]() のみであることを示したい,
ということですね.
のみであることを示したい,
ということですね.