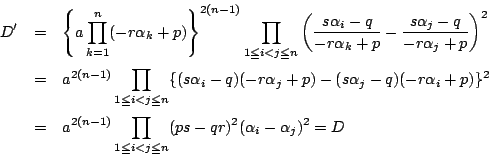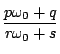 を解にもつ2次方程式を
を解にもつ2次方程式を
耕介 『数論初歩』の「2次無理数の展開と判別式」のところに次の事実が出てきました.
無理数が2次方程式
の解であるとき, これと対等な無理数
を解にもつ2次方程式を
とする. 二つの2次式の判別式を
と
とすると,
である.
ある無理数![]() に対し,無理数
に対し,無理数![]() が
が
![]() であるような整数
であるような整数![]() を用いて
を用いて
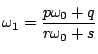 と表されるとき,
この二つの無理数
と表されるとき,
この二つの無理数
![]() は互いに対等であるというのでした.
は互いに対等であるというのでした.
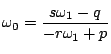 なので,
これをもとの方程式に代入し,
得られた
なので,
これをもとの方程式に代入し,
得られた![]() の満たす2次方程式を決める.
その判別式をとるのですが,証明を読んでみると,
の満たす2次方程式を決める.
その判別式をとるのですが,証明を読んでみると,
![]() が整数であることは使っていません.
要するに,元の2次方程式
が整数であることは使っていません.
要するに,元の2次方程式![]() の
の![]() に,
に,
![]() であるような
であるような![]() によって作られる
によって作られる
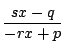 を代入し,分母を払って整理すると
新たな2次方程式
を代入し,分母を払って整理すると
新たな2次方程式
![]() が得られる.
二つの2次式の判別式は変わらない,ということを言っています.
が得られる.
二つの2次式の判別式は変わらない,ということを言っています.
南海
![]() を
を
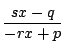 に置きかえて得られた方程式の判別式が,
この変換で変わらないことに気づいたのはすばらしい.
に置きかえて得られた方程式の判別式が,
この変換で変わらないことに気づいたのはすばらしい.
![]() は整数でなくてもよいばかりでなく,
複素数一般でもかまわない.
は整数でなくてもよいばかりでなく,
複素数一般でもかまわない.
数学では,何らかの変換を行ったときに, それに対して不変なものを見出し, 不変なものが作る集合の構造を考えることが,大変重要である. 不変な量,不変な関係を明確にすることが, 数学的現象を考えるうえでもっとも基本的な方針だ.
正確な定義はこれからおこなっていくが, このような変換によって不変な式を一般に不変式という.
耕介
2次方程式![]() から,先の方法で別の2次方程式
から,先の方法で別の2次方程式
![]() を作る.その判別式
を作る.その判別式![]() を,
もとの係数
を,
もとの係数![]() で表すと,結局
で表すと,結局![]() に戻ります.
に戻ります.
一定の係数の変換に対し判別式は不変である,ということですね.
南海 そうだ. 今日は, 高校数学の背景のひとつなっている不変式について, 高校数学と地続きなところから考えはじめよう,
![]() であるような任意の
であるような任意の![]() に対して,
に対して,
![]() を
を
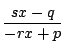 に置きかえ分母を払って2次式を作る.
係数は変化するが,判別式は変わらないという条件を考える.
に置きかえ分母を払って2次式を作る.
係数は変化するが,判別式は変わらないという条件を考える.
![]() が
が![]() を満たすことと,
を満たすことと,
![]() が
が![]() を満たすことは同値であるから,
この条件は,
を満たすことは同値であるから,
この条件は,
![]() であるような任意の
であるような任意の![]() に対して,
に対して,
![]() を
を
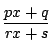 に置きかえ分母を払って2次式を作っても,
判別式は変わらない,という条件と同値だ.
に置きかえ分母を払って2次式を作っても,
判別式は変わらない,という条件と同値だ.
そこで![]() を
を
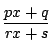 に置きかえ分母を払って
2次式を作ることで不変性を確認していこう.
に置きかえ分母を払って
2次式を作ることで不変性を確認していこう.
2次方程式を
耕介
判別式は![]() です.
です.
南海
この![]() に
に
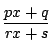 を代入し分母を払って得られる新たな2次方程式を
を代入し分母を払って得られる新たな2次方程式を
耕介
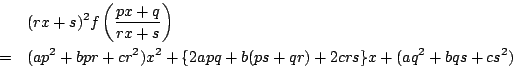
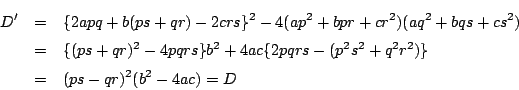
南海
今は変換された係数から直接計算したが,
根の方から考える別解がある.
耕介
![]() は
は
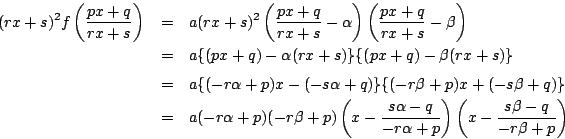
南海 判別式を根で表し不変性を確認してほしい.
耕介
![]() の解と係数の関係から
の解と係数の関係から
![]() ,
,
![]() なので,
判別式は
なので,
判別式は
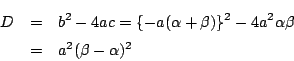
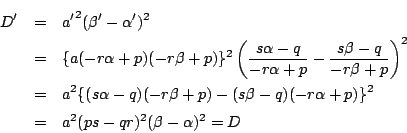
根の変換の方から示すとこのようになりました.
南海 その通りで,この方法はそのまま一般化できる. 判別式というものの定義も,係数からするのではなく, 根からおこなう.
その前に,2007年の入試問題をひとつ紹介しよう.
この問題では方程式を
![]() の代わりに
の代わりに
![]() と置いている.
われわれも後半ではこのように置く.
この2は
と置いている.
われわれも後半ではこのように置く.
この2は
![]() なのだが,
係数をこのようにする方がより複雑なときは計算がきれいになる.
なのだが,
係数をこのようにする方がより複雑なときは計算がきれいになる.
![]() をひとかたまりにして係数の変換を考えると,
これまでの考察との関連を読み取ることができる.
をひとかたまりにして係数の変換を考えると,
これまでの考察との関連を読み取ることができる.
南海
さて一般的に考えるために,多項式の判別式の定義からはじめよう.
耕介 係数はどのようなところからとるのですか.
南海 一つの体を固定すればよいのだが, とくに断らなければ複素数体としよう. または,係数は文字のままであるとしてもよい.
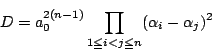
耕介 判別式は,根をどのように入れ替えても変わりません.
南海
そう.あとで詳しく見るが,根の対称式であり,
ちょうど![]() を乗じていることによって,
もとの整式の係数から作られた整式になる.
また,方程式
を乗じていることによって,
もとの整式の係数から作られた整式になる.
また,方程式![]() が重根をもつための必要十分条件が
が重根をもつための必要十分条件が
![]() であることは,判別式の定義から明らかである.
であることは,判別式の定義から明らかである.
例として,![]() の判別式を求めて見てほしい.
の判別式を求めて見てほしい.
耕介 これは『数学対話』「三次方程式」にあります.
この式は見たことがあります.
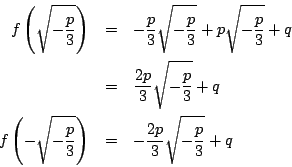
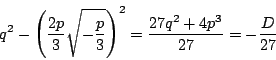
これは2次式で
![]() をとると,
をとると,
![]() .
.
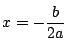 で極.
極値は
で極.
極値は
南海
そう.
さて,判別式は,![]() 個の根の番号をどのようにつけ替えても,変わらない.
つまり
個の根の番号をどのようにつけ替えても,変わらない.
つまり![]() 個の根の対称式である.
次節で基本定理の系1で示すように次のことが成り立つ.
個の根の対称式である.
次節で基本定理の系1で示すように次のことが成り立つ.
このことはここでは認め,判別式の不変性を先に確認しよう.は
の係数
の
次の整式である.
![]() であるような2次行列
であるような2次行列
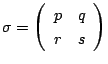 をとり,
をとり,
![]() に対して,
に対して,
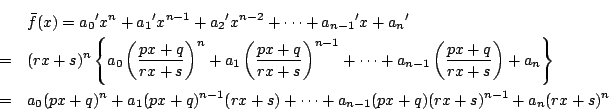
耕介
2次方程式の場合では,関係式(1)が成り立つので,
南海 その通りである. 正確には,根の変換から定まる変換での不変式なので, 方程式の不変式といおう.
南海 2次の場合と同じであるから,証明をやってみてほしい.
耕介 はい.
証明
簡単のため![]() とする.
とする.
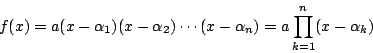
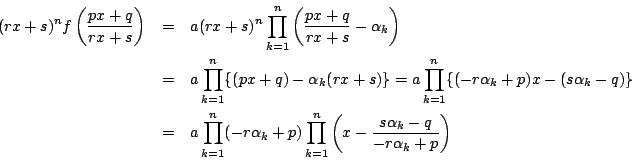
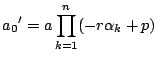 であり,
であり,
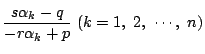 となる.だからその判別式を
となる.だからその判別式を