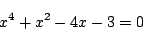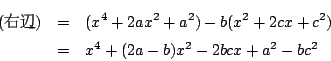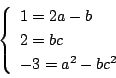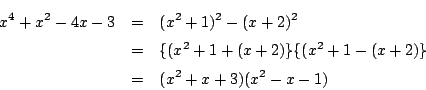次: 別の b の値なら?
上: 4次方程式
前: 4次方程式
耕一 四次方程式の解法になる入試問題を見つけました.
例 1.2.1
[99富山大]
次の問いに答えよ.
- 等式
が 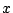 についての恒等式であるように実数
についての恒等式であるように実数 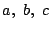 を定めよ.
を定めよ.
- 方程式
の解を求めよ.
南海 よく見つけた.この解法は?
耕一 次のようにしました.
- 与えられた等式の右辺は
したがって,恒等式になるために係数を比較して,
これから 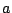 と
と 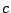 を消去すると
を消去すると
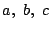 は実数であるから
は実数であるから 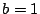 となり
となり
となる.
- (1)から
これから
となる.
Aozora Gakuen
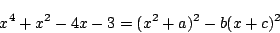
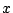 についての恒等式であるように実数
についての恒等式であるように実数 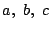 を定めよ.
を定めよ.