次： 四次方程式の一般的解法(1) 上： 4次方程式 前： 入試問題から

別の b の値なら？

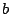耕一　 $b$ は，この問題では実数と指定していますが， 三つある三次方程式の根のどれをとっても四次方程式の解は同じになるはずです． 四次方程式で四つの根（重根は二つと数える）が定まるからです．それを確かめてみました.

南海　ほう,その計算をしたのか.

耕一　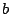 $b$ として

$$b= \frac{-3+\sqrt{9-64}}{2}= \frac{-3+\sqrt{55}i}{2}$$

をとります．このとき

$$a= \frac{1+b}{2}= \frac{-1+\sqrt{55}i}{4}\,,\,c= \frac{2}{b}= \frac{-3-\sqrt{55}i}{16}$$

です．さらに

$$b^{\frac{1}{2}}=\pm \frac{\sqrt{5}+\sqrt{11}i}{2}$$

と二重根号がはずれます．したがって一方の二次方程式は

$$\begin{eqnarray*} &&x^2-b^{\frac{1}{2}}(x+c)+a\\ &=&x^2- \frac{\sqrt{5}+\sqrt... ...\sqrt{11}i}{2}\right\} \left\{ x -\frac{1+\sqrt{5}}{2} \right\} \end{eqnarray*}$$

となります．したがって，二次方程式からでる解の組み合わせがちがうだけで， 四つの解は同じになります.