のとき,以下の問いに答えよ.
-
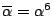 を示せ.
を示せ.
-
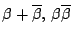 を求めよ.
を求めよ.
-
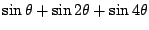 を求めよ.
を求めよ.
耕一 解いてみます.
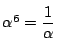 .
一方,
.
一方, 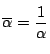 .
.
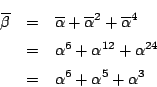
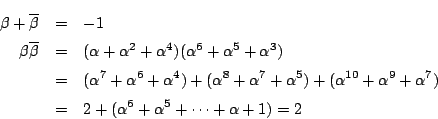
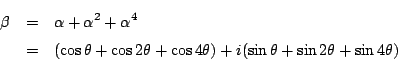
耕一
この問題で
![]() と置いたのですが,
なぜこのようにとるとうまくいくのかわかりません.
と置いたのですが,
なぜこのようにとるとうまくいくのかわかりません.
![]() では
では
![]() が実数になりません.
が実数になりません.
南海 なるほど. 出題者はなぜこのような和を作ったのかということだ.
耕一 同じことを1の11乗根でやってみました.
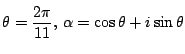 として,
上の場合
として,
上の場合 ![]() ,
,![]() ,
, ![]() ときたのでまねをして,
ときたのでまねをして,
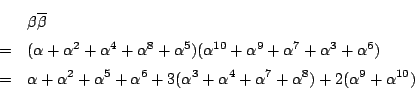
なぜなのでしょう.
南海
このからくりを知るためには, ![]() を構成する
を構成する ![]() のべきを途中で切らずに最後まで書いてみればよい.
のべきを途中で切らずに最後まで書いてみればよい.
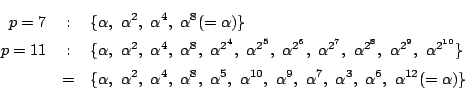
![]() のとき,
のとき, ![]() が
が ![]() の倍数になるのは
の倍数になるのは ![]() が最初だけれど,
が最初だけれど,
![]() のとき,
のとき, ![]() が
が ![]() の倍数になるのは
の倍数になるのは ![]() が最初ではなく
が最初ではなく
![]() ですでになってしまう.だからちょうど
ですでになってしまう.だからちょうど ![]() と
と
![]() の積がきれいになった.
の積がきれいになった.
![]() のときはすべて加えないときれいにならない.
のときはすべて加えないときれいにならない.
「2は11を法とする原始根であるが,7を法としたときは原始根でない」という事実がある. 詳しくは整数論の入門書を読んでみるといいだろう.
そこでせっかく1のべき根に関する質問が出されたので, 1の17乗根を求める方法を紹介しよう.