次： スツルムの定理 上： 1の17乗根 前： 1の17乗根

追加の考察

南海　 ここは『整数論入門』9節「原始根と指数」の知識がいるのだが， $\beta_3,\ \beta_4$ の 分け方の「なぜ」をさらに考えてみよう．

耕一　確かに，あそこでは先生のいわれるようにすればうまくいきましたが， 「なぜ」その用に分ければいいのかはわかりませんでした．

南海　2は $p=17$ に関して原始根ではなかった．つまり

$$\alpha=\cos\dfrac{2\pi}{17}+i\sin\dfrac{2\pi}{17}$$

とするとき，集合

$$\{\ (\alpha^2)^i\ \vert\ i : 自然数\ \}$$

は16個の要素からなるのではなく，ちょうどその半分の8個からできているのだった．

では $\alpha^2$ の代わりに $\alpha^3$ をとるとどうなるだろう．それを調べて， その下に $\alpha^2$ ではどうなるかを書いてみてほしい．

耕一　はい．$3^i$を17で割った余りの表を作ろう．

$$\begin{array}{\vert c\vert\vert c\vert c\vert c\vert c\vert... ...&1&3&9&10&13&5&15&11&16&14&8&7&4&12&2&6\\ \hline \end{array}$$

南海　 これを四つずつで区切り縦に書くと

$$\begin{array}{\vert c\vert c\vert c\vert c\vert} 1&3&9&10\\ 13&5&15&11\\ 16&14&8&7\\ 4&12&2&6 \end{array}$$

一方

$$\left\{ \begin{array}{l} \beta_1=\alpha+\alpha^{13}+\alpha... ...=\alpha^{10}+\alpha^{11}+\alpha^7+\alpha^6 \end{array}\right.$$

となっているだろう．

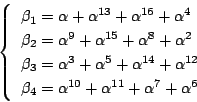
耕一　 するとはじめから3で考えた方が自然だったのですか．

南海　 そうなのだ．縱にとった意味は群論の理解がいる．

17の余りから0を除いた集合

$$(Z/17Z)^{\times}=\{\ 1,\ 2,\ \cdots,\ 16\ \}$$

が積に関して巡回群になり，3が生成元である．

$(Z/17Z)^{\times}$の部分集合 $H=\{\ 1,\ 4,\ 13,\ 16\ \}$ は部分群になる．

$a,\ b\in (Z/17Z)^{\times}$に対して $ab^{-1}\in H$ のとき $a〜b$ と書くことにすると， 互いに〜で結ばれるのが縱にとった四つだ．

部分群 $H$ による類別というのだ．

ではなぜこのようにとるとうまくいったのか．それを解明する理論が「ガロア理論」である． いまは，この背景に前に述べたあのガロアによる理論があることだけ知っておいてほしい．