1の17乗根を求めよう.そこでまず ![]() はどちらの型かな.
はどちらの型かな.
耕一
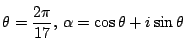 とします.
とします.
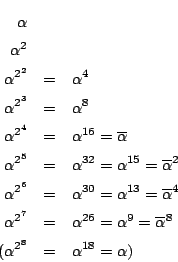
南海
しかも, ![]() と違って
この8個の中にすでに共役なものが組になって入っている.
と違って
この8個の中にすでに共役なものが組になって入っている.
耕一 本当だ.
南海
この8個の和を ![]() ,残り8個の和を
,残り8個の和を ![]() としよう.
としよう.
![]() のときと同様にこの和と積は求まる.
のときと同様にこの和と積は求まる.
耕一 でも計算はたいへんです.
南海
確かに.少し見通しよくすることを考えよう.
今は ![]() を順次
を順次
![]() 乗していったわけだが,
順次
乗していったわけだが,
順次
![]() 乗するとどうなるかな.
乗するとどうなるかな.
耕一
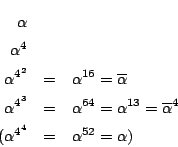
南海
そこでこの4個の和を ![]() ,
,![]() のなかの残りの和を
のなかの残りの和を ![]() とする.
とする.
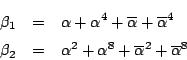
![]() をどのように二つに分けるかが難しいのだ.これまでのことをたどると分かるのだが
規則性をもって
をどのように二つに分けるかが難しいのだ.これまでのことをたどると分かるのだが
規則性をもって ![]() と
と ![]() の各項の指数を3倍することにしよう.
の各項の指数を3倍することにしよう.
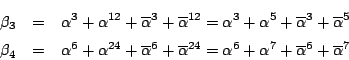
これまでと同様に
つぎに
![]() を求め,
を求め,
![]() ,
,
![]() を決定しよう.
を決定しよう.
耕一 計算します.
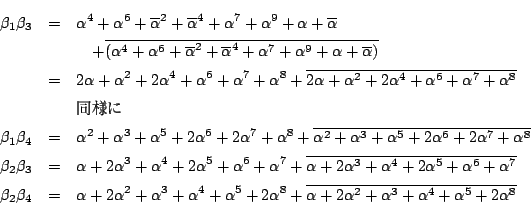
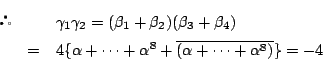
符号は ![]() と同様に決まるので,
と同様に決まるので,
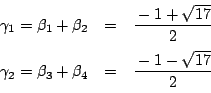
南海
するとだな,
![]() ,
,
![]() が分かれば次の段階に進める.
が分かれば次の段階に進める.
耕一 計算は上と同じですね.結果は
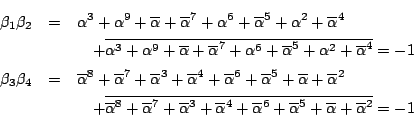
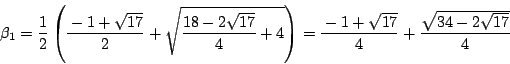
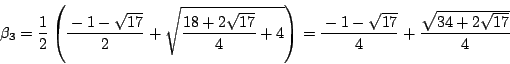
南海
いよいよ大詰め.このように
![]() から
から
![]() が求まっていく.
この
が求まっていく.
この ![]() たちから
たちから ![]() を求めるのだ.
を求めるのだ.
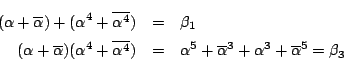
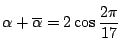 は
は
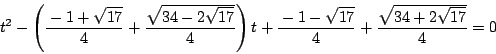
これを計算し整理すると
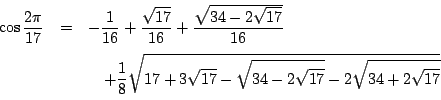
![]() の実部が求まった.虚部は
の実部が求まった.虚部は
![]() ででる.
ででる.
かくして1の17乗根が求まったのだ.
以上の方法は,1796年3月30日,19歳の青年ガウス(C.F.Gauss)が目覚めて起きようとしたときに 発見したものである.そのことが「ガウス日記」に出ている.