- 最高次数の係数が1の整数係数の整式
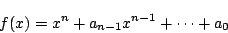
が有理数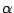 を用いて
を用いて
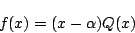
と因数分解された.このとき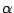 は整数であることを示せ.
は整数であることを示せ.
- さらに係数
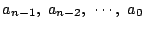 がすべて素数
がすべて素数
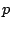 の倍数であるとする.このとき,
の倍数であるとする.このとき,
- 方程式
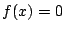 が整数解
が整数解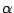 をもてば,
をもてば,
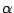 は
は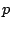 で割り切れることを示せ.
で割り切れることを示せ.
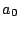 が
が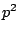 で割り切れなければ,
方程式
で割り切れなければ,
方程式 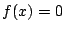 は有理数解を持たないことを示せ.
は有理数解を持たないことを示せ.
- 方程式
これを一通り解きました.
解答
 とおく.
とおく.
よって ![]() は整数である.
は整数である.
![]() が有理数解を持てば(1)からそれは整数解である.
が有理数解を持てば(1)からそれは整数解である.
整数解は ![]() の倍数である.このとき,
の倍数である.このとき,
南海 これはこれで立派な解答だ. 整数係数でしかも最高次数の係数が1である整式は,入試問題のテーマとしてつねに登場する. この解答以外の方法や,この問題の意義について考えてみるのはよいことだ.
別解を考えようとしたというが,どのような方向で考えたのか.
耕一
はい.![]() を方程式の解として考える以外に,整式の因数分解の問題で考えられないか
と思いました.
を方程式の解として考える以外に,整式の因数分解の問題で考えられないか
と思いました.
 とおく.
とおく.![]() で割り切れることは,係数が整数に1次式にすると
で割り切れることは,係数が整数に1次式にすると![]() で割り切れることと同値です.
そこで
で割り切れることと同値です.
そこで
![]()
そこで質問ですが,もし別の方向から上の![]() が整数係数であることが示せたら,
が整数係数であることが示せたら,
![]() から
から![]() がわかります.
がわかります.
南海
実は,整数係数の整式が,有理数係数の整式に因数分解できれば,その係数は整数でとれる
ということがガウスによって示されているのだ.今の場合![]() の係数は互いに素
なので,ここからくくって
の係数は互いに素
なので,ここからくくって![]() 全体にかける整数はないので,
全体にかける整数はないので,![]() 自身が整数係数なのだ.
自身が整数係数なのだ.
それが「原始多項式」の理論だ.
ところで,整式の既約性という問題は数の場合と違ってやや複雑である.
例えば,![]() は有理数の範囲で考えると
は有理数の範囲で考えると
![]() までしか分解できないが,
実数の範囲では
までしか分解できないが,
実数の範囲では
![]() と分解でき,
複素数の範囲では
と分解でき,
複素数の範囲では
![]() と一次式に分解される.
と一次式に分解される.
このようにどの範囲で考えるかで,分解される範囲が異なる.複素数まで考えれば一次式の積に 分解される.
いま考えているのは,「有理数の範囲で因数に分解できれば実は整数の範囲で分解できる」 ことが示せないかということだ.