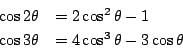
南海 チェビシェフの多項式は大変重要なテーマだ.基礎と応用についてまとめよう.
三角関数に倍角公式というものがある.
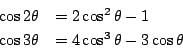
右辺は![]() の多項式になっている.
の多項式になっている.![]() として, これを
として, これを
![]() とおく.
とおく.
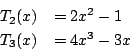
一般に
ところで倍角公式はド・モアブルの定理と二項定理から求まる.
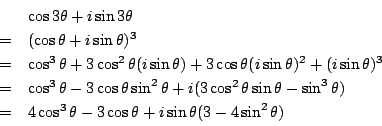
耕一 三角関数の倍角公式は普通は加法定理から求めます.
南海
加法定理は,極形式で表された複素数の積公式
これはまた偏角を0から ![]() にとることを定めておけば
にとることを定めておけば
耕一 いつも思うのですが,上の偏角の公式は 対数と同じ形ですね.
それには理由があって,実は
耕一
だから ![]() とすると
とすると
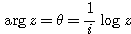
南海
複素数 ![]() に関する
に関する![]() の意味を
定めなければならないのだが,基本的にはそういうことだ.
の意味を
定めなければならないのだが,基本的にはそういうことだ.
さて今日の本題に戻って,いくつかの入試問題を考えよう.
設定が少し違う以外次の問題も同じものだ.
これらは普通にやれば数学的帰納法でやるところだ.しかし次節で複素数で考える.