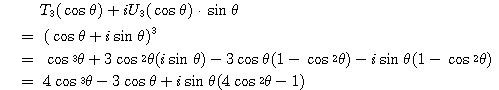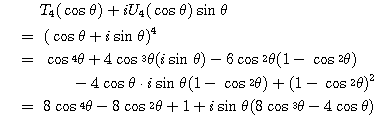- すべての実数
 に対し
に対し
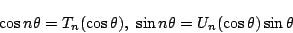
をみたし,係数がともにすべて整数である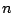 次式
次式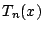 と
と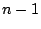 次式
次式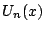 が
存在する.最高次数の項の係数は
が
存在する.最高次数の項の係数は 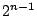 である.
である.
-
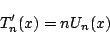
が成り立つ. 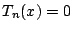 となる
となる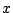 は
は
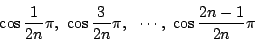
また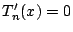 となる
となる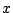 は
は
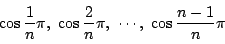
-
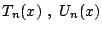 はいずれも次の漸化式を満たす.
はいずれも次の漸化式を満たす.
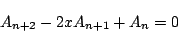
南海 これを証明しよう.
耕一 少しずつやってみます (1) ド・モアブルの定理と二項定理により,
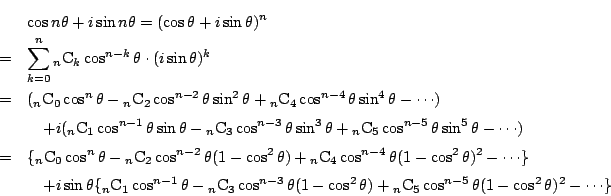
![]() が偶数か奇数かで虚数部の最後の項の書き方が違うので,このようにしましたがいいでしょうか.
が偶数か奇数かで虚数部の最後の項の書き方が違うので,このようにしましたがいいでしょうか.
南海 十分意味がつたわるのでいいと思う.
耕一 これから,
![]() における
における![]() の係数は,
の係数は,
(2)
![]() の両辺を
の両辺を![]() で微分すると,
で微分すると,
(3)
![]() の範囲で考えると,
の範囲で考えると, ![]() とおけて,
とおけて,
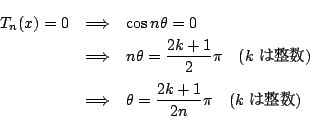
次に,
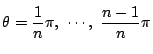 に対して,
に対して,
(4)
耕一 (4)は 3項間漸化式を作るのですね.
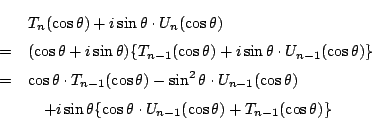
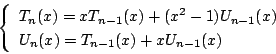
これから漸化式を作ります.
南海 ここはケイレイ・ハミルトンの定理を活用した作り方でやってみよう.
耕一 すると
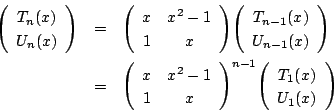
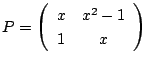 はケーリー・ハミルトンの定理により,
はケーリー・ハミルトンの定理により,
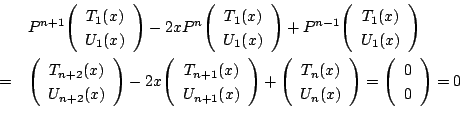
南海 以上で証明はできた.実際の式を作っておくことは大切だ.
耕一 はい.
![]() より,
より,