教科書にはどのように書かれているかな.
耕一
数学Iでは,二次方程式 ![]() の「解」とは,
放物線
の「解」とは,
放物線 ![]() と
と ![]() 軸の共有点の
軸の共有点の ![]() 座標の値と定義されています.
座標の値と定義されています.
そしてそれは
南海
するとここでいわゆる重解の場合,いくつあるのかに関して混乱が生じる.
![]() 軸との共有点という立場に立てば1つだし,
「解の公式」からいえば
軸との共有点という立場に立てば1つだし,
「解の公式」からいえば
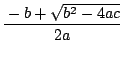 と
と
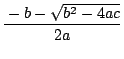 の2つあってそれらが同じ値になる,ということになる.
の2つあってそれらが同じ値になる,ということになる.
1つしかないのか,同じものが2つあるのか.
同じものが2つなら1つではないか,というのはすでに共有点の個数という考え方に とらわれているからで,「白球2つ」といえば「白球1つ」と明確に異なるように, 同じものが2つあることは,1つあることとは明確に別である.
ところが2次方程式 ![]() の解は1つなのか,2つなのかが,
教科書の定義では答えられないのだ.
の解は1つなのか,2つなのかが,
教科書の定義では答えられないのだ.
耕一 確かにはっきりしません.それに方程式の虚数解のことを考えると, 軸との共有点という定義は意味がなくなります.
南海
そうだ.同じ高校数学で,虚数を習うと通用しなくなるような定義を数Iでして,
どうするのかということだ.虚数解まで考えれば,
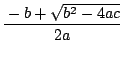 と
と
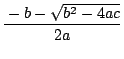 を「解」としなければならない.
そうしておいて重解の場合に戻ると重解とは「2つが同じになっている場合」になり,
を「解」としなければならない.
そうしておいて重解の場合に戻ると重解とは「2つが同じになっている場合」になり,
![]() 軸との共有点という定義にそぐわない.
軸との共有点という定義にそぐわない.
はっきりさせるためには「解」と「根」を使い分けなければならない.
結論的にいえば,二次方程式の重解の場合,「1つしかない」のが「解」であり, 「同じものが2つある」のが「根」である.
異なる概念を混同しているのが今の高校教科書である.
「根」は root から来ている言葉だ.
「根」という言葉は今の高校数学では「根号」とか「平方根」というところに残っているだけだ.
しかし
![]() という記号はもともと root の r から来ているのだから,
毎日「根」は使っている.
という記号はもともと root の r から来ているのだから,
毎日「根」は使っている.
「根」は「根っこ」であり「大地」である. こんなすばらしい言葉を高校数学から追放した現在の教科書の罪は深い.
また,大学に入って習う数学では「根」という. そのときとまどわないようにするためにもここではっきりとさせておこう.
![]() 次方程式
次方程式
またこれらの中には同じものがあることもある.
それに対して解とは何か.「方程式を満たすもの」で,実質は集合
だから![]() 次方程式は
次方程式は![]() 個以下の解をもつ,
あるいは解集合の要素の個数は
個以下の解をもつ,
あるいは解集合の要素の個数は ![]() 以下である,といえる.
以下である,といえる.
2次方程式![]() では
では
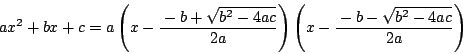
今は教科書では「2次方程式の解の公式」というが, われわれの高校時代は「二次方程式の根の公式」といった.
また「解と係数の関係」というが,二次の場合,二次式の因数分解
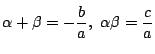 を導くのだから,
これは定義からして「根と係数の関係」だ.
を導くのだから,
これは定義からして「根と係数の関係」だ.
また,重なっているのは「根」なのだから「重根」というのが正しい. ここまでは教科書にあわせて「重解」と使ってきたが,今後は「重根」といおう.
以下ここではこのように「根」と「解」を使い分ける.
耕一 学校でも使い分けるべきでしょうか.
南海 こういう言葉はもっと大切にしてもらいたい. 教科書自身が間違っているところなので, 使い分けなければならない,とまで高校生諸君には言えない. 青空学園で学んだ人はそれをおさえたうえで, 実際の入試問題などでは出題者の使い方にあわせておいてよい. 入試問題を解くというのは,出題者の問いに答えるということだから, 出題者以上に厳格である必要はない.
ただ大学生になって代数学を習えばそこでは「解」と「根」が使い分けられているので その点は心得ておいてもらいたい.