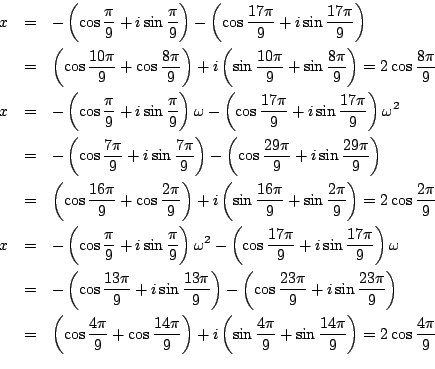次: 三次方程式の判別式
上: 3次方程式
前: 三次方程式を解く(その1)
南海
上の例は二次方程式を解く部分で実数解をもったが,そこで虚数解をもつ場合もやってみよう.
三次方程式として
を上と同様にやってみよう.
耕一
はい.
となる 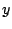 と
と 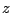 が見つかればよい.
が見つかればよい.
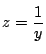 なので
なので
これから
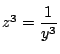 なので
なので 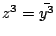
とする.極形式では
である.
よって,同様の考察から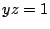 となるように
となるように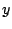 と
と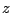 の3乗根を一つずつ選ぶ.いずれを選んでも
同じ3根が得られることに注意しよう.
の3乗根を一つずつ選ぶ.いずれを選んでも
同じ3根が得られることに注意しよう.
としてよい.したがって
できました.今は具体的に考えたので作れましたが一般に,三次方程式が
重解をもつのか,虚数解をもつのか判別することはどうするのですか.
Aozora Gakuen
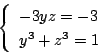
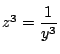 なので
なので