
この証明では,先に1点で交わることを証明してもよいし, 先の定理の証明の考え方で,あとから垂心に関する問題として証明してもよい.
証明1
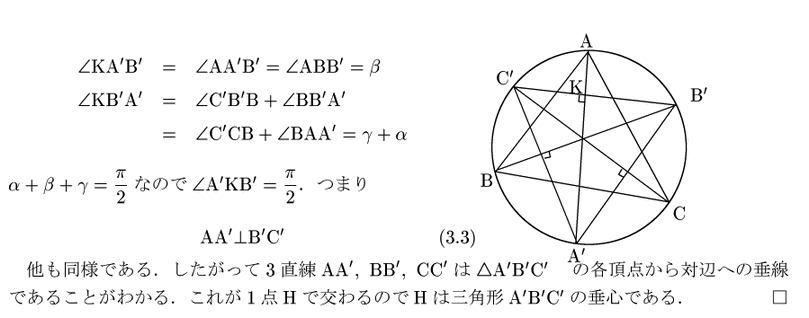
証明2 (証明1の後半と同様に,先に(3.3)を示す.その後次のように,3直練AA',BB',CC'が1点で交わることを示す.)

これを踏まえてフォイエルバッハの定理を証明しよう.
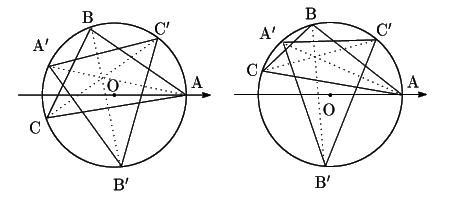
補題1と同様に,各頂角の二等分線と接円の交点を
![]() とおく.この三点の座標を求める.
円周角と中心角の関係を見ることにより
とおく.この三点の座標を求める.
円周角と中心角の関係を見ることにより
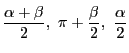 となる.
これは鈍角三角形でも同じである.つまり
となる.
これは鈍角三角形でも同じである.つまり
補題1によって
![]() の垂心が
の垂心が
![]() の内心である.
補題1の証明と同様にして,
の内心である.
補題1の証明と同様にして,
![]() の垂心として
の垂心として
![]() の内心を求めると,
の内心を求めると,
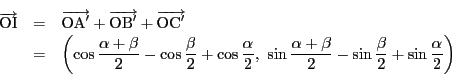
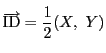 と置くと,
と置くと,
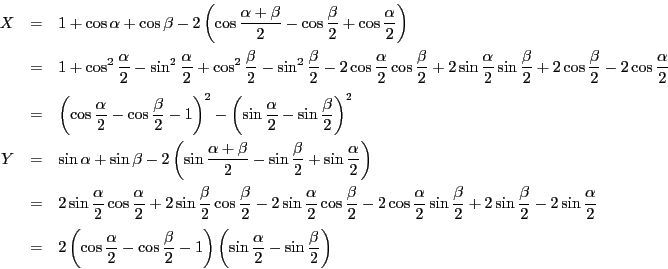
次に内接円の半径
![]() は内心
は内心![]() と直線
と直線![]() との距離である.
直線
との距離である.
直線![]() の方程式は
の方程式は
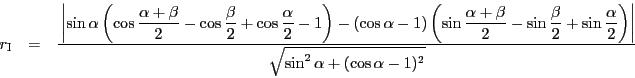
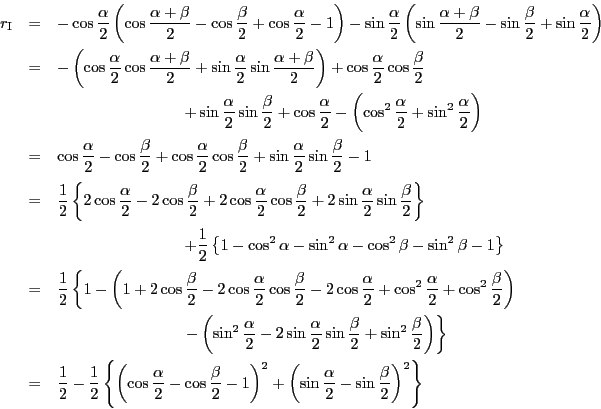
よって
傍接円の場合.
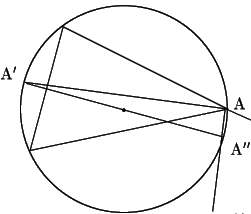
![]() の二等分線と外接円の交点を
の二等分線と外接円の交点を![]() ,
,
![]() の補角の二等分線と外接円の交点を
の補角の二等分線と外接円の交点を
![]() とする.
とする.
 なので,点
なので,点![]() は点
は点![]() の原点
の原点![]() に関する
対称点である.これから
に関する
対称点である.これから
![]() が
が![]() 軸の正の方向となす角はそれぞれ
求めると
軸の正の方向となす角はそれぞれ
求めると
頂角
![]() の二等分線と
の二等分線と
![]() の補角の二等分線が
の補角の二等分線が
![]() の垂心となる点で交わることは補題1と同様に示される.
この交点が傍接円の中心である.
この交点を
の垂心となる点で交わることは補題1と同様に示される.
この交点が傍接円の中心である.
この交点を![]() とおく.
とおく.

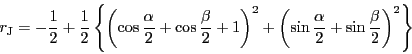
耕一 たいへんな計算ですが,計算の方向ははっきりしています.
南海 そうなのだ.これをいくつもの補助線を引いて示すのは, 職人技的な技巧が必要だ. フォイエルバッハの定理の証明は『幾何学』(長友次郎吉著)に四つ載っている. また『幾何の有名な定理』(矢野健太郎著)には複素数平面において,複素数の計算による証明がある. 三角関数の計算による本証明はいずれにも載っていないが,本質的には複素数の計算によるものと同じだ.