next up previous 次: 反転 上: 反転と円環問題 前: 反転と円環問題

和算の問題

太郎　 いくつかの入試問題で反転に出会いました． 最近では2007年の阪大文理3番が反転の問題です．『別解研究』 に載っているように解答がいくつもあることがわかりました． ただ入試問題としては，だいたい出てくる形は同じです． 一方の点がある曲線上や領域内を動くとき， 反転された点の軌跡や存在領域を求める，というものです． 結局は座標で解くことが多いです． つまり，反転の位置にある二点の座標について，その関係式を導いたうえで， 一方の点の条件から他方の点の条件を導くということになります．

南海　 それらの入試問題は 図形を反転したらどのような図形に変わるかということを問うている． その意味で反転そのものを問うている． 実は反転には，反転を用いた図形問題の解法という重要な応用がある．

日本では江戸時代から数学の研究が盛んで，体系的な書物もあれば，各地の草の根の研究家が自分で考えたことを額にして奉納した算額というのもある．その研究および記述の方法は当然西洋のそれとは違う．その方法を和算という．しかしそれが同じ数学的現象を研究するものであったことは変わりない．

和算の解法は必ずしも反転を用いたものではないのだが， 和算の問題には反転を用いることで比較的簡明に解けるものがある． 西洋でも古くから知られてきた円環問題や， 球の連鎖に関する問題に反転を応用することを考えていこう．

     右の図を見てほしい． 径というのは直径だ．      図は『精要算法　巻之下』（藤田定資著） に載っている

\begin{displaymath} 外円径20，甲円径5\ のとき丙円の径は\ ? \end{displaymath}

という問題である． 大きい円(外円)と小さい円(丁円)の間に 甲円，乙円が互いに外接して並んでいる． このとき二つの円の径から他の径を求めよ，ということだ．

太郎　 たくさん余弦定理を書いて連立すればできそうですが．

南海　 上記の本ではそのようにして解かれているようだ． 和算では三角比は用いない．三平方の定理を駆使する． 実際にやってみれば大変なことに気づく．

    この問題を一般化してとらえよう． いくつかの円が外円には内接し他の円とは外接するようにおかれている．

円$O_1$が円$O_2$を含んで定まっている． 円 $C_1,\ C_2,\ \cdots,\ C_n$ が円$O_1$に内接，円$O_2$に外接し， さらに $i=1,\ 2,\ \cdots,\ n-1$に対し $C_i$が$C_{i+1}$に外接し， $C_n$は$C_1$に外接している．

このような円の集合をシュタイナーの円環， 略して「円環」ともいう． ヤーコブ・シュタイナー (Steiner，1796〜1863)は，スイスの幾何学・数学者である．


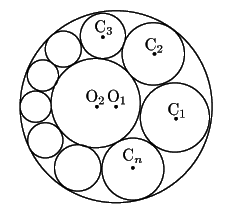太郎　 図を描いてみます． はじめにかいたときは最後の円は重なってしまい，この円列は円環になりません． なんとか少し大きさを変えて描きました． 円 $O_1,\ O_2,\ C_1,\ C_2,\ \cdots,\ C_n$の中心を $\mathrm{O}_1,\ \mathrm{O}_2,\ \mathrm{C}_1,\ \mathrm{C}_2,\ \cdots,\ \mathrm{C}_n$で表しています．

南海　 このような状態になったとき，つまり円環が成立したとき，次のことが成り立つ． ただし$O_1,\ O_2$の半径を$R,\ r$，中心間の距離を$d$とする．

\begin{displaymath} d^2=(R-r)^2-4Rr\tan^2\dfrac{\pi}{n} \end{displaymath}
太郎　 この等式には$n$個の小円の半径は出てきません．

南海　 いいところに気づいた． 実は小円の半径は関係ない． 次のことが成り立つ．

$n$個の円環が一つできれば， 最初の円$C_1$をどこにとっても順に外接させていけば， $C_n$は$C_1$に外接する．

太郎　 一つ存在すれば，どこからはじめても出来る， という形の定理を見たことがあります． 「ポンスレの閉形定理」です．

南海　「ポンスレの閉形定理」は，「2つの円の一方に内接し他方に外接する$n$角形が1つ存在すれば，いずれかの円の任意の点を指定しても，その点を頂点の一つとする（あるいは一つの辺がその点で接する）$n$角形が存在する」であった．

命題は類似している．しかし二つの定理は異なる範疇に属する．

太郎　それはどういうことですか．

南海　ポンスレの定理は射影幾何の定理であるが，シュタイナーの定理は射影幾何の定理ではない．いいかえると，ポンスレの定理は，ある2円で成立すれば，それを射影変換で移した2つの二次曲線で成立し，逆も言える．

シュタイナーの定理が成立する2円と$n$個の円を射影変換すると，一方に内接し他方に外接し互いに接する$n$個の2次曲線ができるが，シュタイナーの定理は，一般の二次曲線では証明されていない．つまり，一方に内接し他方に外接する任意の二次曲線で同様のことが成り立つことが示せているわけではない．

あとでシュタイナーの定理を反転によって同心円にうつして証明するが，円に関する反転は射影変換ではない．

Aozora Gakuen