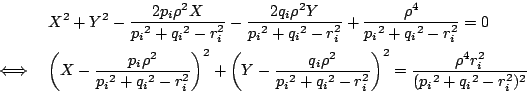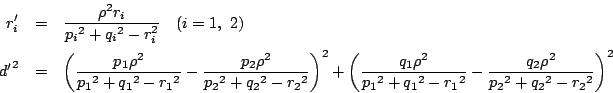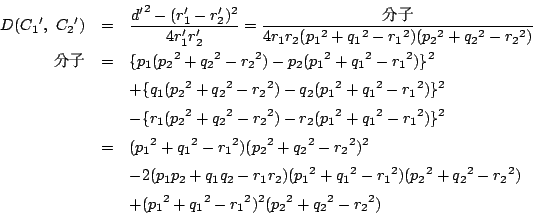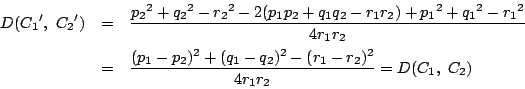反転とはどのようなことか.
太郎
平面上の点![]() を中心とする半径
を中心とする半径
![]() の円がある.
の円がある.
![]() から半直線上に2点
から半直線上に2点
![]() をとる.
をとる.
南海
その通り.この円を反転の定円,![]() を反転の中心,
を反転の中心,
![]() を反転の半径という.
点
を反転の半径という.
点![]() がある図形を描くとき,
それに対応して
がある図形を描くとき,
それに対応して![]() もある図形を描く.
それらの図形も互いに反転であるという.
もある図形を描く.
それらの図形も互いに反転であるという.
太郎 反転は平面から平面への一対一の写像です.
南海
いや,厳密に言うと平面から反転の中心![]() を除かなければならない.
を除かなければならない.
太郎
そうか.![]() は無限の彼方に行ってしまうのだ.
は無限の彼方に行ってしまうのだ.
南海
だから逆に無限遠点![]() を考え
を考え
反転に関する基本事項は次のことだ. 証明は2007年の阪大文理3番と同じくいろんな方法がある.
 ■
■
太郎 慣れた座標でやってみたいですが場合に分けるのがめんどうです.
南海
まとめてやるために![]() の方程式を
の方程式を
証明
反転の中心を原点におき,反転の定円の半径を![]() とする.
点
とする.
点
![]() と
点
と
点
![]() がこの円に関して反転であるとする.
すると
がこの円に関して反転であるとする.
すると
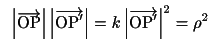
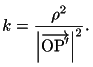 これから成分で書いて
これから成分で書いて
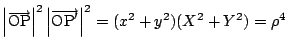 も成り立つ.
点
も成り立つ.
点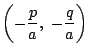 にあり,
反転した円の中心
にあり,
反転した円の中心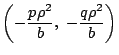 にあるので,
にあるので,
□
南海 それでいい. この論証は図形的にするより座標の方が簡明なのだが, しかしすべてを座標でやるのは,逆に大変なのだ. 一般に円に関する論証では,円周角の関係するものを座標ですると複雑になる. そのときは図形の論証の方が見通しよい. ここからは図形的に考えていこう.
次のようなことを確認しておきたい.
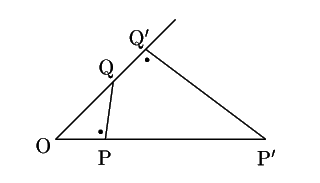 2)
2)
つまり四角形
![]() は円に内接する.
は円に内接する.
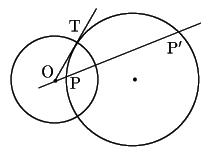 3)
3)
![]() を通る円と点
を通る円と点![]() に関する方べきの定理から,
に関する方べきの定理から,
![]() からこの円への接線を
からこの円への接線を![]() とすると,
とすると,
![]() である.
一方
である.
一方
![]() なので,
なので,
![]() .つまり
.つまり![]() は反転の定円上にもあり,
この二円は点
は反転の定円上にもあり,
この二円は点![]() で直交している.
で直交している.
逆に反転の定円に直交し,交点が![]() とすると,
とすると,![]() は
円の接線である.
は
円の接線である.![]() を通り円に割線を引き,
交点を
を通り円に割線を引き,
交点を
![]() とする.
方べきの定理から
とする.
方べきの定理から
![]() となり,
となり,
![]() と
と![]() は互いに反転である.
よって円は,この反転でそれ自身にうつる.
は互いに反転である.
よって円は,この反転でそれ自身にうつる.
4) 円![]() と
と![]() が反転しており,
反転の中心
が反転しており,
反転の中心![]() を通る
割線
を通る
割線![]() 上の点
上の点
![]() と
と
![]() をとる.
をとる.
![]() をそれぞれ接線とする.
方べきの定理から
をそれぞれ接線とする.
方べきの定理から
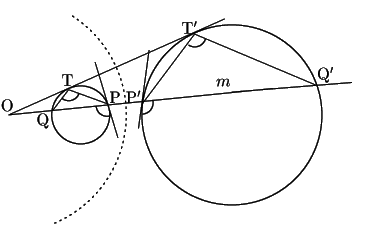

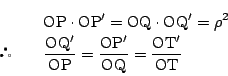
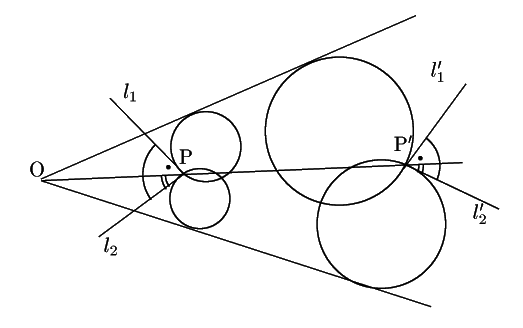
図より
交点での接線![]() のなす角をこの順の方向に計った角が
のなす角をこの順の方向に計った角が![]() とするとき,
交点での接線
とするとき,
交点での接線
![]() のなす角をこの順の方向に計った角は
のなす角をこの順の方向に計った角は![]() である.
である.
5)
![]() から
から![]() ,
,![]() までの接線の長さがそれぞれ
までの接線の長さがそれぞれ
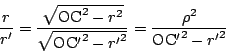
□
南海 さらに,4)に追加すると,相交わる円だけではなく,円と直線,直線と直線の場合についても, 交点でなす角は反転によって大きさが変わらず,向きだけ逆になる. これはそれらの直線に交点で接する円をとり, それらの図形の反転をとることによって分かる.
一点注意であるが,二つの円が反転の関係のとき,反転中心からこれら二円に共通接線が引け, 接点もまた同じ反転で対応する.しかし,円の中心はこの反転で対応するものではない.
反転は複比を符号を含めて保存する.
証明 定理2の2)と同様に方向まで考えて
これらのことからただちに導かれるものとして,パップスの円環定理を紹介しなければならない.
太郎 パップスって,『数学対話』「パップスの定理」のパップスですか.
南海 そうだ.歴史的なことはそれを読んでもらうとして,定理そのものは別のものだ.
系 1 (パップスの円環定理)
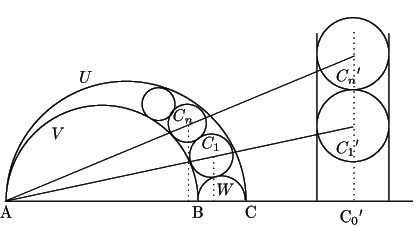 直線
直線![]() 上に3点
上に3点
![]() がこの順に並んでいる.
がこの順に並んでいる.
![]() を直径とする半円
を直径とする半円![]() を描きその中に
を描きその中に
![]() を直径とする半円
を直径とする半円![]() を描く.
を描く.
![]() とし
とし
![]() に対して
に対して
![]() が定まったとき,
が定まったとき,
![]() に内接し
に内接し![]() と
と![]() に外接する円
に外接する円![]() を描きその中心を
を描きその中心を
![]() ,半径を
,半径を![]() ,
,
![]() と
と![]() との距離を
との距離を![]() とする.
とする.
このとき
![]() に対して
に対して
この円![]() の集合を「アルキメデスのアルベロス(靴屋のナイフ)円列」という.
パップスはいくつかの過程を経てようやくにこれを示したといわれている.
ところがこのように反転の図形的な性質を用いることで簡明に示すことができる.
しかしまた座標計算も捨てがたい.
次の定理は機械的な計算でできる.
の集合を「アルキメデスのアルベロス(靴屋のナイフ)円列」という.
パップスはいくつかの過程を経てようやくにこれを示したといわれている.
ところがこのように反転の図形的な性質を用いることで簡明に示すことができる.
しかしまた座標計算も捨てがたい.
次の定理は機械的な計算でできる.
証明 反転の中心を原点にとり,反転の半径を
円の方程式に
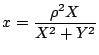 ,
,
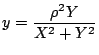 を代入し整理する.
を代入し整理する.