太郎
二円![]() の方程式を
の方程式を
![]() とする.
ただし円の方程式であるから
とする.
ただし円の方程式であるから![]() の係数は1にとる.
このとき,方程式
の係数は1にとる.
このとき,方程式
![]() とし,
とし,
![]() を円
を円![]() の外部の点とする.
このとき
の外部の点とする.
このとき![]() は点
は点![]() から円に引いた接線の長さの平方になる.
このことを用いて根軸の図形的な意味を考えることができる.
つまり,円の外部の点
から円に引いた接線の長さの平方になる.
このことを用いて根軸の図形的な意味を考えることができる.
つまり,円の外部の点![]() から
から![]() に接線が引けるとき,接点を
接点
に接線が引けるとき,接点を
接点
![]() とすれば
とすれば
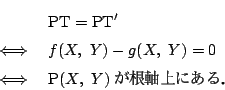
![]() が
が![]() で,かつ方程式
で,かつ方程式
南海 最後の部分は91年の東大後期の問題でもあるのだが, 次にも使うので必要十分性の補題として証明しておいてほしい.
太郎 はい.
![]() と
と![]() の直交しているとする.
三平方の定理より
の直交しているとする.
三平方の定理より
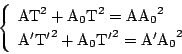
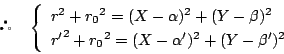
逆に根軸上の接線が引ける位置に![]() があれば,
共有点をもつような半径
があれば,
共有点をもつような半径![]() をとり,
式変形を逆にたどることで
をとり,
式変形を逆にたどることで![]() と
と![]() の直交性がわかる.
□
の直交性がわかる.
□
南海
円の集合があってそのどの二つの根軸をとってもすべて一致するとき,
この円の集合を根軸によって定まる円束という.
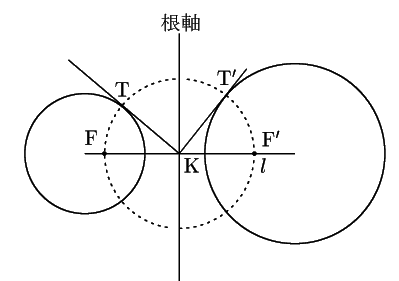 二円
二円![]() が共有点をもたないとする.
この二円の根軸と二円
が共有点をもたないとする.
この二円の根軸と二円![]() の中心を結ぶ直線
の中心を結ぶ直線![]() との交点を
との交点を![]() とする.
とする.
![]() から
から
![]() への接線の長さ
への接線の長さ
![]() に対して
に対して
![]() 上の点で
上の点で
太郎 どうして焦点というのですか.
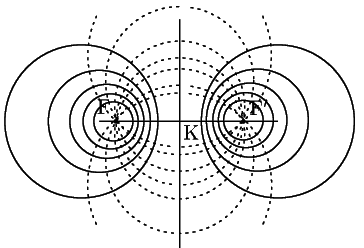 南海
根軸が同じ円束をかいてみると図のように半径が小さくなると焦点に収束していく円列が得られる.
また,焦点を通る円を描いてみるとこれらはすべて円束と直交している.
このように二つの種類の円の集合が得られる.
南海
根軸が同じ円束をかいてみると図のように半径が小さくなると焦点に収束していく円列が得られる.
また,焦点を通る円を描いてみるとこれらはすべて円束と直交している.
このように二つの種類の円の集合が得られる.
この問題は今回はここでおいておくが,後日また考えたい.
定理 5
互いに交わらない二円![]() がある.
二円の焦点
がある.
二円の焦点![]() を中心とする反転でこれら二円は同心円にうつる.
■
を中心とする反転でこれら二円は同心円にうつる.
■
一方,二円![]() の中心と反転の中心は二円
の中心と反転の中心は二円![]() の焦点を結ぶ直線
の焦点を結ぶ直線![]() 上にあるので,
円
上にあるので,
円
![]() の中心も
の中心も![]() 上にある.
上にある.
従って円
![]() の中心は
の中心は![]() 上かつ
上かつ![]() 上にあるので,
その交点に一致する.つまり円
上にあるので,
その交点に一致する.つまり円
![]() の中心は一致する.
□
の中心は一致する.
□
本定理は,一方の円が他方に含まれる場合も同様である.
南海 焦点による反転をもちいて定理4の別証明をしよう.
反転によって,
![]()
![]() に
なるとする.この四点は
に
なるとする.この四点は![]() の反転円
の反転円![]() の周上にある.
の周上にある.
![]() と
と![]() が直交するので,
が直交するので,![]() と
と
![]() は直交している.
は直交している.
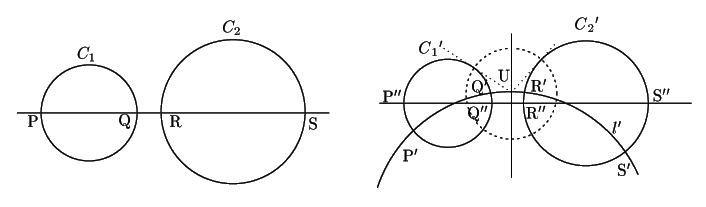
定理3によって
次に
![]() の根軸と
の根軸と![]() の交点を
の交点を![]() とする.
とする.
![]() から
から
![]() に接線を引き接点までの長さ
に接線を引き接点までの長さ![]() をとる.
をとる.
![]() を中心とし
を中心とし![]() を半径とする円
を半径とする円![]() に関して反転をおこなう.
に関して反転をおこなう.
![]() は
は![]() と直交しているので,この反転でそれ自身にうつる.
と直交しているので,この反転でそれ自身にうつる.
![]() は直線
は直線![]() にうつるが
にうつるが![]() の
の
![]() と直交しているので,
これが
と直交しているので,
これが
![]() の中心を通る直線である.
の中心を通る直線である.
![]() がそれぞれ
がそれぞれ
![]() にうつるとすると,
これが
にうつるとすると,
これが![]() と
と
![]() の交点である.
の交点である.
再び定理3によって
太郎 反転と根軸を組みあわせて用いることで, 簡明に出来るのですね.