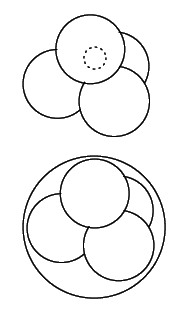
 空間に五つの球がある.その半径を
空間に五つの球がある.その半径を
 空間に五つの球がある.その半径を
空間に五つの球がある.その半径を
![]() とする.
互いに外接しているとき,これらの五つの半径の間に
とする.
互いに外接しているとき,これらの五つの半径の間に
が成り立つ.四つの球が互いに外接し,これらが第五の球に内接しているとき,
これらの五つの半径の間に
が成り立つ.
太郎 こうなると余弦定理でやっていくのはほとんど無理です.
南海 和算家はこのような場合も結論を得ていた. まったく驚くべきことである.
太郎 さらに一般の次元に拡張できるのですか.
南海 できる.そのために![]() 次元空間について,
直接必要ではないことも含めてまとめておこう.
次元空間について,
直接必要ではないことも含めてまとめておこう.
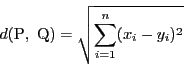
![]() 次元ユークリッド空間はまたベクトル空間でもあり,
ベクトルとしての和・差,および実数倍が定まることは,
2次元3次元の場合と同じである.
特に点
次元ユークリッド空間はまたベクトル空間でもあり,
ベクトルとしての和・差,および実数倍が定まることは,
2次元3次元の場合と同じである.
特に点![]() と原点
と原点
![]() を始点とするベクトル
を始点とするベクトル
![]() が同一視できることなども,
2次元3次元の場合と同じである.
ベクトル空間と見るときは
が同一視できることなども,
2次元3次元の場合と同じである.
ベクトル空間と見るときは![]() の要素を
の要素を
![]() や
や
![]() のようにも表す.
矢線はつけないことも多い(「線型代数の考え方」ではつけていない)が,
ベクトルであることを明確にするためここでは
のようにも表す.
矢線はつけないことも多い(「線型代数の考え方」ではつけていない)が,
ベクトルであることを明確にするためここでは
![]() 式の書き方をしよう.
式の書き方をしよう.
このことに注意すると,
二点![]() ,
,![]() の距離
の距離
![]() はベクトル
はベクトル
![]() の大きさでもある.
の大きさでもある.
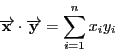
太郎
ベクトル
![]() ,
,
![]() とすると
とすると
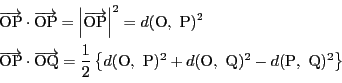
南海 平面を考える前にまず![]() の部分空間
を定義しなければならない.
の部分空間
を定義しなければならない.
![]() の部分集合
の部分集合![]() が
が![]() の加法と定数倍に関して
それ自体ベクトル空間であるとき,
の加法と定数倍に関して
それ自体ベクトル空間であるとき,
![]() を
を![]() の部分空間という.
の部分空間という.
言い換えると
太郎 平面ベクトルにおいて原点を通る直線, 空間ベクトルにおいて原点を通る直線や 原点を通る平面が,このような条件を満たすのではないでしょうか.
南海 そうだ. さて部分空間![]() が与えられたとき,
が与えられたとき,
太郎 平面ベクトルで![]() が原点を通る直線なら
が原点を通る直線なら![]() はそれと直交し原点を通る直線になります.
空間ベクトルで
はそれと直交し原点を通る直線になります.
空間ベクトルで![]() が原点を通る直線なら
が原点を通る直線なら![]() はそれと直交し原点を通る平面になります.
はそれと直交し原点を通る平面になります.
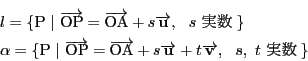
太郎
![]() とするとこの条件は
とするとこの条件は
南海 超平面![]() をベクトル
をベクトル
![]() の集合と見れば,
このベクトルの加法を加法とする
の集合と見れば,
このベクトルの加法を加法とする![]() 次元のベクトル空間を
点
次元のベクトル空間を
点![]() 通るように平行移動したものである.
だから平面という概念は,
通るように平行移動したものである.
だから平面という概念は,
![]() 次元空間の部分空間(を平行移動したもの)と一般化することができる.
次元空間の部分空間(を平行移動したもの)と一般化することができる.
南海 以上の準備のもとで円定理を一般の場合に拡張する. それが次の定理だ.
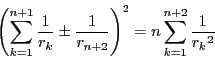
太郎 とんでもなく難しいように思われます.
南海 このような円定理がどのようなところからやってくるのかを考えなおすことで, ![]() 次元へ一般化する方法を見出そう.
次元へ一般化する方法を見出そう.
(1)
4個のベクトル
![]() ,
,
![]() ,
,
![]() ,
,
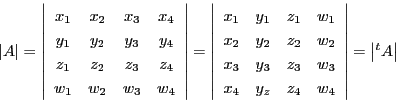
![]() に対し,行列
に対し,行列![]() と行列式
と行列式![]()
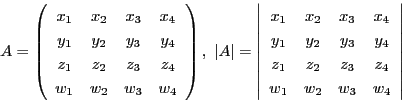
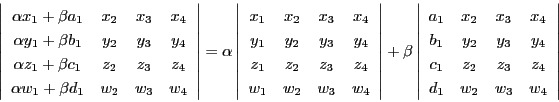
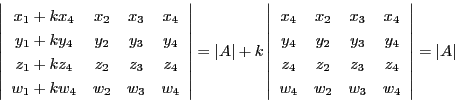
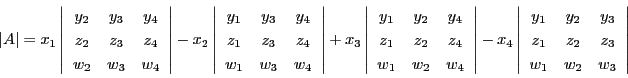
この書は東北大学のサイト『東北大学和算ポータル』で全ページ閲覧することができる.