![]() のときは次のようになります.
のときは次のようになります.
1次元,つまり直線上の三つの円がある.
互いに接しているとき,半径を
![]() とすると
とすると
これを計算すると,
これが定理の内容です.
![]() のときの等式はこのようになります.
のときの等式はこのようになります.
ところで一次元の円とは何ですか?
南海 円の定義ではどうなるか.
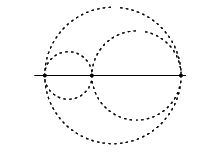 太郎 定点からの距離が一定な点の集合です. ということは直線上では二点です.二点の組が一次元の円ですね. すると接するというのは,そのいずれかの点を共有し,中心間の距離が半径の和か差になるということです.
結局,三つの円の関係が図のようになるときのみ可能です.よって
太郎 定点からの距離が一定な点の集合です. ということは直線上では二点です.二点の組が一次元の円ですね. すると接するというのは,そのいずれかの点を共有し,中心間の距離が半径の和か差になるということです.
結局,三つの円の関係が図のようになるときのみ可能です.よって![]() .が成り立ちます.
.が成り立ちます.
南海 これらの円の中心となる三点が同一直線上にあるということそのものだ. そしてそれらの点の間の距離が,対応する半径の和や差に他ならない.
一次元の場合のこの定理をどのように導くか? 一般化の可能な方法はないのか? それを考えてみよう.
つまり中心となる三点が一直線上にあるということと,点の間の距離が半径の和や差であるということから,その関係を半径の間の関係で表せば,一次元の公式が出るのではないか.
平面上に置かれた三点は,一般には三角形を形成する.
中心となる三点を
![]() ,
,
![]() ,
,
![]() とする.
このとき
とする.
このとき
![]() の面積
の面積![]() はどのようになるか?
はどのようになるか?
太郎
![]() ,
,
![]() なので
なので
南海 行列式で書くと?
太郎
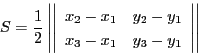
南海 面積も向きをつけて考えるのだが,今はその必要がないので, このように絶対値で考えていくことにしよう.
行列式の性質から
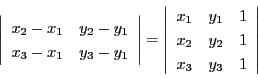
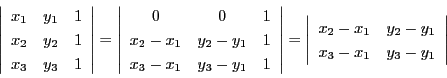
南海
![]() の面積といえばもう一つは何か?
の面積といえばもう一つは何か?
太郎 ヘロンの公式です.三辺の長さで面積を表すものです.
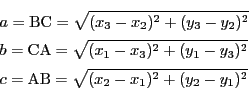
南海 これを展開すると
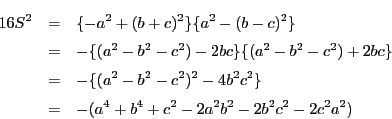
この先の一般化のために,ヘロン公式を三点の座標の方から作って見よう.
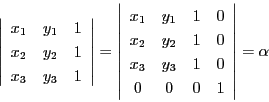

太郎 行列式の積は,行列の積の行列式なので
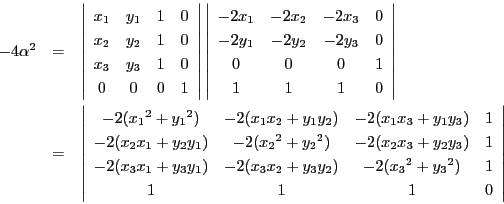
南海 ここで, 第四列に![]() ,
,![]() ,
,![]() をかけて
それぞれ第一列,第二列,第三列に加える.
また
第四行に
をかけて
それぞれ第一列,第二列,第三列に加える.
また
第四行に![]() ,
,![]() ,
,![]() をかけて
それぞれ第一行,第二行,第三行に加える.
をかけて
それぞれ第一行,第二行,第三行に加える.
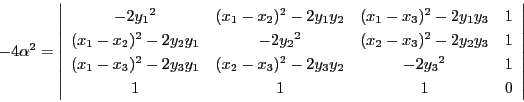
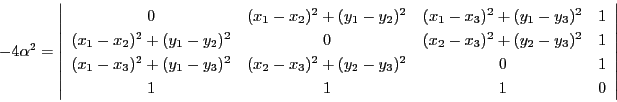
つまり
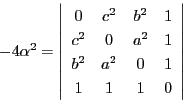
太郎
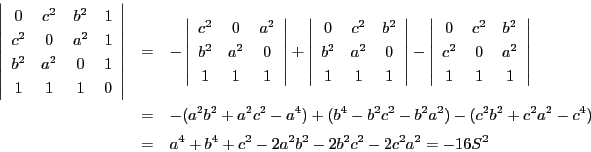
南海 考えてみれば, 面積公式もヘロンの公式も同じ
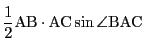 から作っているのだから,
一方から他方が出ても不思議ではない.
まとめると
から作っているのだから,
一方から他方が出ても不思議ではない.
まとめると
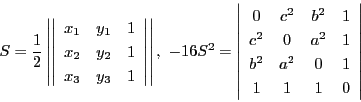
太郎 そうなのですか. 三点が一直線上にあるための必要十分条件はでます. 三点
![]() が同一直線上にあるのは,
ベクトル
が同一直線上にあるのは,
ベクトル
![]() ,
,
![]() が一次従属であることですから,その行列式
が一次従属であることですから,その行列式
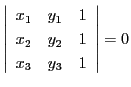 となるときです.つまり
となるときです.つまり
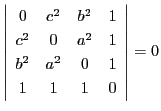 です.
これが三点が同一直線上にあるための必要十分条件です.
です.
これが三点が同一直線上にあるための必要十分条件です.
南海 円が接するとき,中心間の距離は半径の和か差である. 点
![]() を中心とする円が互いに外接し,
点
を中心とする円が互いに外接し,
点![]() を中心とする円に内接しているとしよう.
を中心とする円に内接しているとしよう.
三点を中心とする円の半径をそれぞれ
![]() とすると,
とすると,
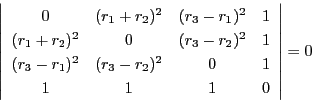
太郎 これから円定理の![]() の場合を導くのですね.
しかし式変形の方向がわかりません.
の場合を導くのですね.
しかし式変形の方向がわかりません.
南海 第四行に![]() をかけ第
をかけ第![]() 行から引く.
第四列に
行から引く.
第四列に![]() をかけ第
をかけ第![]() 列から引く.
この結果
列から引く.
この結果
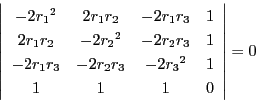
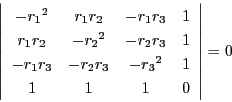
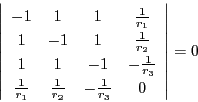
太郎
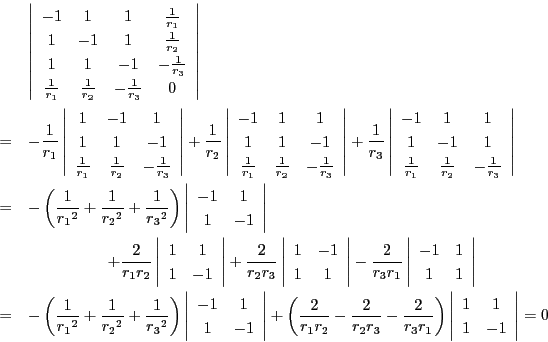
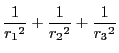 を加えて
を加えて
南海 そういうことだ.