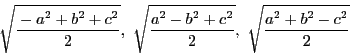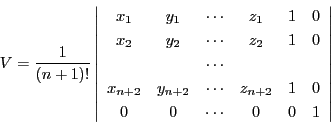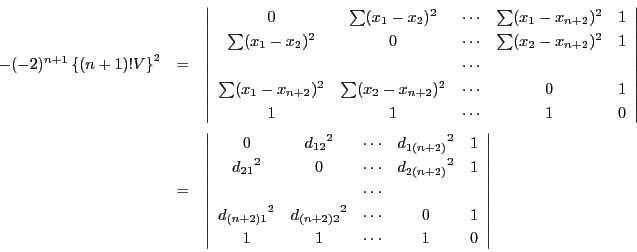上: デカルトの円定理と一般化
前: 一般の場合の証明
上: デカルトの円定理と一般化
前: 一般の場合の証明
南海 ヘロンの公式で与えられる面積公式が値0になる場合は,それらの頂点が同一直線上にあるときである.このことを導きに,円定理を,頂点の位置が一般の位置にはない場合の関係式として導いた.つまりわれわれの考察の交差点にはヘロンの公式があった.
そこで,ここでヘロンの公式の空間版である四面体の体積を辺長で表す公式を導いてみよう.計算法はこれまでの行列の変形を見習いながらも,自己完結的に導く方法でやってみよう.
四面体の4頂点を
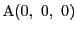
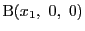 ,
,
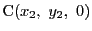 ,
,
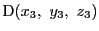 ,
として一般性を失わない.このとき四面体ABCDの体積
,
として一般性を失わない.このとき四面体ABCDの体積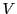 は
は
となる.ここで辺長を
とする.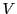 をこれらの辺長で表したものが,求める公式である.
そこでこれまでの方法にならって
をこれらの辺長で表したものが,求める公式である.
そこでこれまでの方法にならって
とおく.
よって
ここで第5行と第5列に
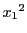 ,
,
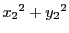 ,
,
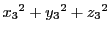 をかけ,
それぞれ第2行,第3行,第4行,および
第2列,第3列,第4列に加える.行列式の値は変わらない.これによって
をかけ,
それぞれ第2行,第3行,第4行,および
第2列,第3列,第4列に加える.行列式の値は変わらない.これによって
よって
これが四面体の体積を辺長で表す公式であり,ヘロンの公式の三次元への拡張である.
ここで等面四面体の場合を考える.
このときは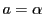 ,
,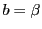 ,
,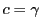 であるから
であるから
これから
となり,この場合は因数分解された形になる.
これは辺長が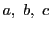 の等面四面体が,3辺が
の等面四面体が,3辺が
の直方体に埋め込め,
その直方体の体積の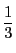 が四面体の体積であることから直接にも示される.
が四面体の体積であることから直接にも示される.
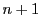 元空間におかれた
元空間におかれた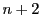 個の点を
個の点を
とする.
頂点を結ぶ線分は
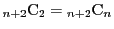 本あり,
そのうちの
本あり,
そのうちの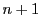 本でできる
本でできる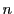 次元の超平面が
次元の超平面が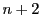 枚できる.
これらで囲まれた
枚できる.
これらで囲まれた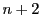 超面体の体積
超面体の体積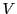 は
は
である.
この体積公式を用いれば,
が一般の場合のヘロンの公式である.
3次元の公式もこれからも導かれるが,
体積の考察を高校範囲に収めるため,
先のように四面体を一般性を失わない範囲で体積がわかりやすい形で座標空間においた.
2014-07-06
![]()
![]() ,
,
![]() ,
,
![]() ,
として一般性を失わない.このとき四面体ABCDの体積
,
として一般性を失わない.このとき四面体ABCDの体積![]() は
は
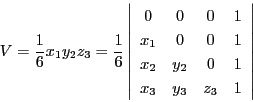
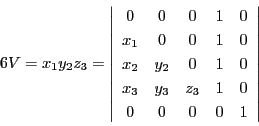
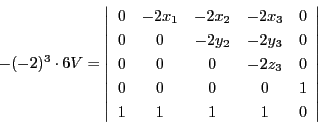
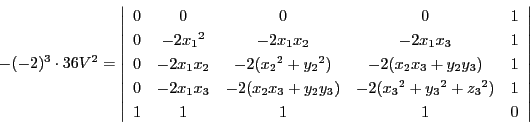

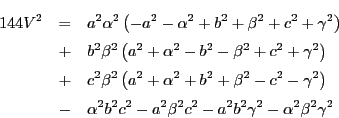
![]() ,
,![]() ,
,![]() であるから
であるから
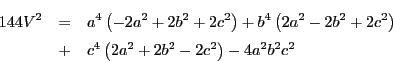
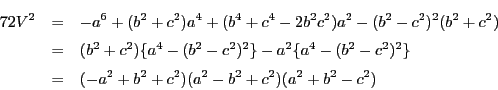
![]() の等面四面体が,3辺が
の等面四面体が,3辺が