

 次: ヘロンの公式の一般化
上: デカルトの円定理と一般化
前: ヘロンの公式再考
次: ヘロンの公式の一般化
上: デカルトの円定理と一般化
前: ヘロンの公式再考
南海 以上の考察はそのまま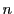 次元に一般化される.
面積公式から考察をはじめたが,
面積公式そのものは必要ない.
一次独立性を判定する行列式が0であることのみを用いる.
次元に一般化される.
面積公式から考察をはじめたが,
面積公式そのものは必要ない.
一次独立性を判定する行列式が0であることのみを用いる.
太郎 ここまでのことをまとめると
- まず
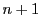 次元空間におかれた
次元空間におかれた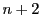 個の点が,
個の点が,
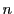 次元空間上にある条件を座標の行列式で表す.
次元空間上にある条件を座標の行列式で表す.
- その条件を,点間の距離の行列式で表す.
- 点間の距離の行列式に半径の和か差を代入する.
- その結果得られる半径の間の関係式が
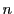 次元の場合の球定理である.
次元の場合の球定理である.
となります.
南海 そのとおりだ.
さて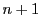 次元空間で同様のことを行う.
そのために,
次元空間で同様のことを行う.
そのために,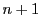 次元空間の座標を
次元空間の座標を
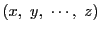 として,
として,
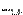 の部分にも座標変数があり合計で
の部分にも座標変数があり合計で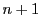 個であるとしよう.
個であるとしよう.
太郎 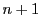 元空間におかれた
元空間におかれた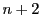 個の点を
個の点を
とする.これらの点が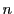 次元空間上にあるための必要十分条件は
次元空間上にあるための必要十分条件は
です.
である.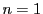 の場合と同様に計算する.
の場合と同様に計算する.
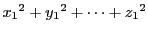 や
や
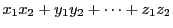 などをそれぞれ
などをそれぞれ
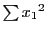 ,
,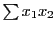 のように表す.
のように表す.
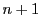 個の座標にわたる和である.
個の座標にわたる和である.
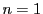 の場合と同様に
の場合と同様に
となる.
ここで,
第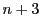 列に
列に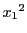 ,
,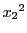 ,…,
,…,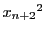 をかけて
それぞれ第一列,第二列,…,第
をかけて
それぞれ第一列,第二列,…,第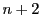 列に加える.
また
第
列に加える.
また
第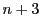 行に
行に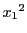 ,
,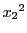 ,…,
,…,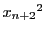 をかけて
それぞれ第一行,第二行,…,第
をかけて
それぞれ第一行,第二行,…,第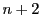 行に加える.
各座標成分についてこれを行うことで
行に加える.
各座標成分についてこれを行うことで
を得る.
ここで
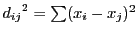 とおく.
とおく.
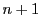 次元空間におかれた
次元空間におかれた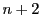 個の点が
個の点が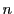 次元空間上にある必要十分条件
は
次元空間上にある必要十分条件
は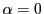 であったので,等式
であったので,等式
が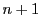 次元空間におかれた
次元空間におかれた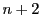 個の点が
個の点が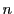 次元空間上にある条件を,
点間の距離の関係式で表したものである.
次元空間上にある条件を,
点間の距離の関係式で表したものである.
南海 ここに
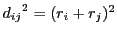 を代入する.
ただし
を代入する.
ただし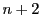 番目の球に他の球が内接する場合
番目の球に他の球が内接する場合
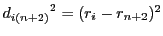 を代入する.
この場合は
を代入する.
この場合は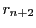 を負にとることにすれば,
場合に分ける必要がない.
を負にとることにすれば,
場合に分ける必要がない.
太郎
第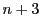 行に
行に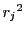 をかけ第
をかけ第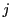 行から引く.
第
行から引く.
第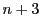 列に
列に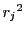 をかけ第
をかけ第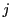 列から引く.
この結果
列から引く.
この結果
第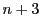 行,第
行,第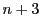 列に2をかけ,
そのうえで各列を2で割っても
列に2をかけ,
そのうえで各列を2で割っても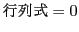 は変わらない.
は変わらない.
そのうえで
第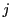 行を
行を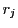 で割り,
第
で割り,
第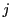 列を
列を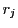 で割る.この結果
で割る.この結果
これを展開することにより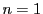 の場合と同様に
の場合と同様に
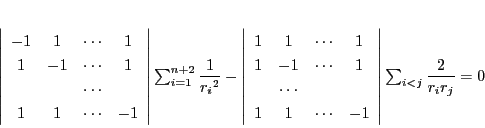 |
(1) |
が得られるはずです.
南海 結論はその通りである.実際,次のようになる.
この結果,等式(1)が得られる.
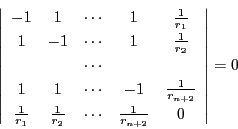
ここで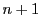 次行列式
次行列式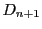 と
と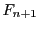 を
を
とおく.等式(1)は
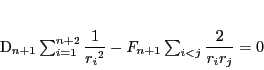 |
(2) |
となる.
これから
よってすべての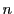 で
で
等式(2)より
両辺に
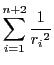 を加えて
を加えて
を得る.
すでに指摘したように,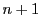 この球が
この球が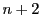 番の球に内接しているときは,
番の球に内接しているときは,
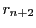 を負とすることによって示される.
以上で定理2が示された.
□
を負とすることによって示される.
以上で定理2が示された.
□
和算では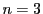 のときの公式を用いて,
六球連鎖の問題を解いたのだ.
互いに接する3個の球
のときの公式を用いて,
六球連鎖の問題を解いたのだ.
互いに接する3個の球
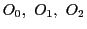 のどれにも接する球の連鎖
のどれにも接する球の連鎖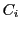 について,まず
について,まず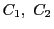 で球定理をつかえば
で球定理をつかえば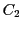 の半径が決まる.
これから
の半径が決まる.
これから
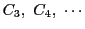 と順に決定してゆけば
と順に決定してゆけば で終わることが示せる.
これは膨大な計算になるはずだ.
で終わることが示せる.
これは膨大な計算になるはずだ.


 次: ヘロンの公式の一般化
上: デカルトの円定理と一般化
前: ヘロンの公式再考
次: ヘロンの公式の一般化
上: デカルトの円定理と一般化
前: ヘロンの公式再考
2014-07-06
![]() 次元空間で同様のことを行う.
そのために,
次元空間で同様のことを行う.
そのために,![]() 次元空間の座標を
次元空間の座標を
![]() として,
として,
![]() の部分にも座標変数があり合計で
の部分にも座標変数があり合計で![]() 個であるとしよう.
個であるとしよう.
![]() 元空間におかれた
元空間におかれた![]() 個の点を
個の点を
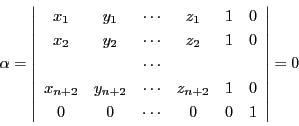
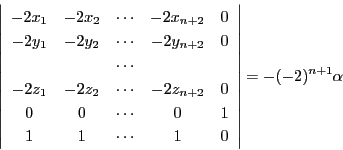
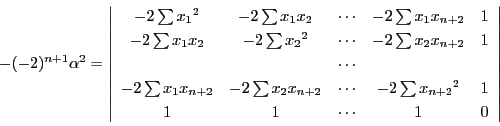
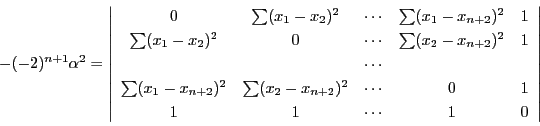
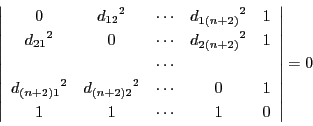
![]() を代入する.
ただし
を代入する.
ただし![]() 番目の球に他の球が内接する場合
番目の球に他の球が内接する場合
![]() を代入する.
この場合は
を代入する.
この場合は![]() を負にとることにすれば,
場合に分ける必要がない.
を負にとることにすれば,
場合に分ける必要がない.
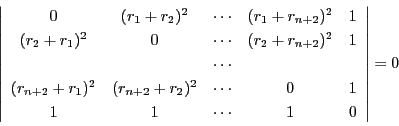
![]() 行に
行に![]() をかけ第
をかけ第![]() 行から引く.
第
行から引く.
第![]() 列に
列に![]() をかけ第
をかけ第![]() 列から引く.
この結果
列から引く.
この結果
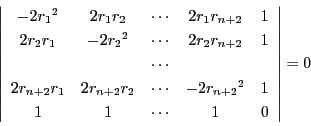
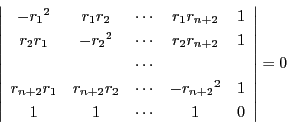

![]() 次行列式
次行列式![]() と
と![]() を
を
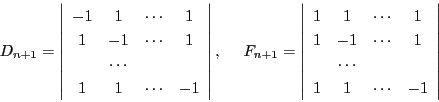
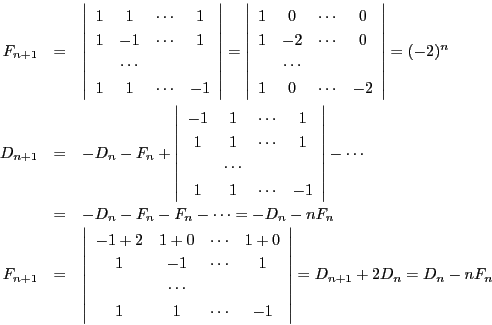
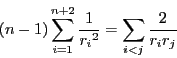
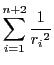 を加えて
を加えて
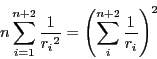
![]() のときの公式を用いて,
六球連鎖の問題を解いたのだ.
互いに接する3個の球
のときの公式を用いて,
六球連鎖の問題を解いたのだ.
互いに接する3個の球
![]() のどれにも接する球の連鎖
のどれにも接する球の連鎖![]() について,まず
について,まず![]() で球定理をつかえば
で球定理をつかえば![]() の半径が決まる.
これから
の半径が決まる.
これから
![]() と順に決定してゆけば
と順に決定してゆけば![]() で終わることが示せる.
これは膨大な計算になるはずだ.
で終わることが示せる.
これは膨大な計算になるはずだ.