次： シュタイナー楕円 上： シュタイナー楕円 前： シュタイナー楕円

入試問題の分析

南海　おもしろい問題がある．解いてみてください．

例 1.2.1       ［00東大前期理系］

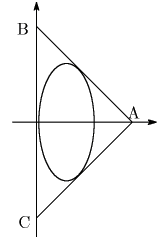
AB=AC，BC=2     の直角二等辺三角形 ABC の各辺に接し，ひとつの軸が辺 BC に平行な楕円の面積の最大値を求めよ．

拓生　 やってみます．

解答

$\mathrm{A}(1,\ 0)$ ， $\mathrm{B}(0,\ 1)$ ， $\mathrm{C}(0,\ -1)$ と $xy$ 座標平面におく．

$\bigtriangleup \mathrm{ABC}$ に内接し軸が $\mathrm{BC}$ と平行な楕円は対称性から原点で $y$ 軸と接する．したがって，

$$\dfrac{(x-a)^2}{a^2}+\dfrac{y^2}{b^2}=1$$

とおける．

この楕円が点 $(1-t,\ t)$ で線分 $\mathrm{AB}$ に接しているとする．楕円のこの点での接線は

$$\dfrac{(1-t-a)(x-a)}{a^2}+\dfrac{ty}{b^2}=1$$

である．これが $x+y=1$ と一致する．つまり

$$\dfrac{1-t-a}{a^2}x+\dfrac{t}{b^2}y=1+\dfrac{1-t-a}{a}$$

が $x+y=1$ と一致する．よって，

$$\dfrac{1-t-a}{a^2}=\dfrac{t}{b^2}=1+\dfrac{1-t-a}{a}$$

これから $t$ を消去して $a$ と $b$ の関係式を求めると

$$b^2=1-2a$$

となる．

楕円の面積は半径１の円を $x$ 軸方向に $a$ 倍， $y$ 軸方向に $b$ 倍したものであるから， $\pi ab$ である．

$$\pi ab=\pi \sqrt{a^2-2a^3}$$

$f(a)=a^2-2a^3$ とおく． $0<a<\dfrac{1}{2}$ である．

$$f'(a)=2a-6a^2$$

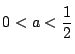より $a=\dfrac{1}{3}$ で極大かつ最大である．

面積の最大値は

$$\dfrac{\sqrt{3}\pi}{9}$$

である．□

拓生　 ずいぶんあっさりとした解答です．

南海　 いや．大切なことは，必ず解ける方法でやることだ．この場合，内接する条件を書きあげ， その条件をみたしつつ面積を最大にする場合を求めればよいのだから，この方法でいいのだ．

拓生　 この問題はこれだけのことなのでしょうか．

南海　 楕円とくれば当然その焦点を考えねばならない．焦点の座標はどうなるかな．

拓生　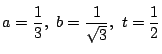 $a=\dfrac{1}{3},\ b=\dfrac{1}{\sqrt{3}},\ t=\dfrac{1}{2}$ ですから計算すると，

$$\left(\dfrac{1}{3}\,,\,\pm \dfrac{\sqrt{2}}{3}\right)$$

です．

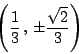
南海　 ここで平面を複素数平面とする．焦点は 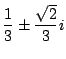$\dfrac{1}{3}\pm \dfrac{\sqrt{2}}{3}i$ となるわけだが，三つの頂点は

$$1,\ i,\ -i$$

だ．これらを解とする三次方程式は何かな．

拓生　 それは

$$(x-1)(x-i)(x+i)=x^3-x^2+x-1=0$$

です．

南海　 ここで方程式の部分を微分すると

$$3x^2-2x+1=0$$

拓生　 あっ．この二次方程式の二解が焦点になっている！

南海　 そうなのだ．実は次のことが成り立つ．