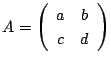 を用いて,
を用いて,
拓生 東大の問題は三角形に内接する楕円で面積最大のもの を求めよ,ということでした.それを一般化したのが(2)ですね.
南海 これは直観的には次のように考えればよい.
正三角形に内接する面積最大の楕円は各辺の中点で接する円である.
正三角形から2方向への拡大で任意の三角形と相似な三角形が得られ,辺の中点で内接する楕円は 再び辺の中点で内接する楕円になり,相対的な大小関係は変わらないからである.
これをもう少し厳密にいうと,今は習わなくなった一次変換が必要だ.
行列
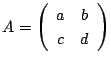 を用いて,
を用いて, ![]() 平面の点
平面の点 ![]() から点
から点 ![]() への変換
への変換
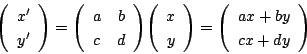
![]() とするとベクトルからベクトルへの変換でもある.
とするとベクトルからベクトルへの変換でもある.
これは次の性質を持つ.
さらに
![]() のとき次のことが成り立つ.
のとき次のことが成り立つ.
二次曲線
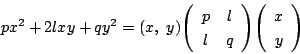
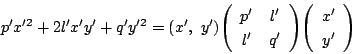
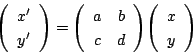
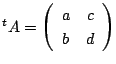 とおくと
とおくと
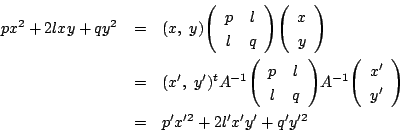
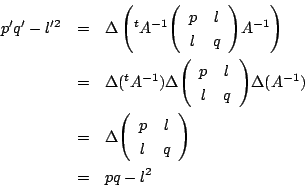
よって一次変換で二次曲線の ![]() の値は不変.
の値は不変.
適当な一次変換で二次曲線が標準形になったとする.標準形は ![]() のときである.
のときである.
よって ![]() となる.
これは
となる.
これは
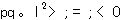 に応じて楕円,放物線,双曲線,であることを示し,
さらに一次変換で楕円は楕円に移ることを示している.
に応じて楕円,放物線,双曲線,であることを示し,
さらに一次変換で楕円は楕円に移ることを示している.
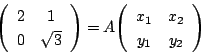
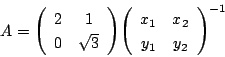
2.の証明
南海 次のようにして,三角形に内接する楕円で面積最大のものがシュタイナー楕円であることが示される.
面積=周長×半径÷2なので周長で考えればよい. 周長を最短にする三角形が正三角形でなければ等しくない2辺をとり, その2辺が等しくなるよう第3の辺を引き直した三角形はそれよりも周長が短くなるので矛盾.
正三角形に内接する楕円を任意にとる. この楕円を正三角形の内接円に一致させる一次変換を正三角形に施す. すると変形後の三角形は(2)によりもとの正三角形よりも面積は大きい. 楕円は内接円よりも面積が小さいことがわかる.