例 1.4.1
長さ1の線分を,両端が放物線 ![]() の上にあるように動かすとき,
その線分の通過領域を求めよ.
の上にあるように動かすとき,
その線分の通過領域を求めよ.
直線がある条件をみたしながら動くとき,その通過する領域を求める問題は,入試問題でも頻出だ. これはどのような方法があるのだったかな.
拓生 線分の通過領域は,結局,放物線上にある長さが1離れた2点を結ぶ直線 を考え,その通過領域のうち放物線の周と上部にある部分をとれば,求まるはずです.
長さが1離れた2点を
![]() とすると,
条件と直線は次のようになります.
とすると,
条件と直線は次のようになります.
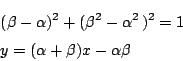
それで,ここから![]() を消去すると,
を消去すると,
南海 そこですこし発想を変えてみよう.