南海
実数 ![]() に対し,
に対し,
![]() とすると,これはどのような図形を表しますか.
とすると,これはどのような図形を表しますか.
拓生
式を整理すると,
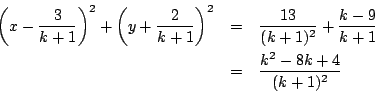
![]() のとき円になり,
のとき円になり, ![]() のとき1点,さらに
のとき1点,さらに
![]() のときは空集合,です.
のときは空集合,です.
南海
![]() が大きくなるとどうなりますか.
が大きくなるとどうなりますか.
拓生
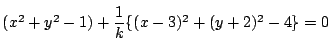 で
で
![]() ですから,
ですから, ![]() に近づいていく.
に近づいていく.
南海 そうです.まとめると
| 表す図形 | |
| 円 | |
点
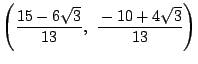 |
|
| 空集合 | |
点
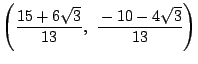 |
|
| 円 | |
|
|
|
| 円 | |
| 直線 |
|
| 円 | |
このように媒介変数 ![]() の一次式で定まる曲線族を「束」と呼びます.問題は,
この「束」を特徴づける幾何的な性質はどのようなことか,と言うことです.
の一次式で定まる曲線族を「束」と呼びます.問題は,
この「束」を特徴づける幾何的な性質はどのようなことか,と言うことです.
拓生 私の質問とどのような関係があるのでしょうか.