これを,
![]() を円
を円![]() とし,
とし,![]() を放物線
を放物線 ![]() を考える.
ここで定数は条件
を考える.
ここで定数は条件
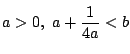 を満たしているとする.
を満たしているとする.
![]() 座標が
座標が ![]() と異なる
と異なる ![]() 上の点
上の点
![]() から
から ![]() にひとつの接線をひき,
その延長が再び
にひとつの接線をひき,
その延長が再び ![]() と交わる点を
と交わる点を
![]() とする.
とする.
![]() から
から ![]() に
に ![]() とは異なる接線をひき,
その延長が再び
とは異なる接線をひき,
その延長が再び ![]() と交わる点を
と交わる点を ![]() とする.
とする.
![]() から
から ![]() に
に ![]() とは異なる接線をひき,
その延長が再び
とは異なる接線をひき,
その延長が再び ![]() と交わる点を
と交わる点を ![]() とする.
とする.
拓生 やってみます.
解答
(1)
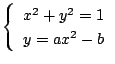 において
において![]() を消去する.
を消去する.
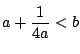 のときは
のときは
![]() とする.直線
とする.直線![]() の式は
の式は
(2)
点
![]() とする.
とする.
これは点![]() を通り
を通り![]() に接する直線を2本引いたとき,その接線の
に接する直線を2本引いたとき,その接線の![]() との交点の座標である.
との交点の座標である.
![]() となることは,
となることは,![]() が再び
が再び![]() と接すること,すなわち
と接すること,すなわち
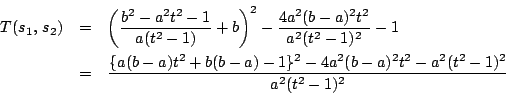
(3)
対称性から![]() となるために点
となるために点![]() の
の![]() 座標は1でなければならない.
座標は1でなければならない.
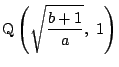 とする.
とする.
直線![]() が円
が円![]() に接すればよい.
に接すればよい.![]() の傾きは
の傾きは
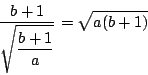
南海 名古屋大学の問題は確かにこの条件を満たしてる.
拓生 はい.
![]() のとき(2)の条件は
のとき(2)の条件は
(4)
(2)の条件式![]() を変形する.
を変形する.
![\begin{eqnarray*}
H(t)&=&a^2\{(b-a)^2-1\}t^4+2[ab(b-a)^2-a(b-a)-2a^2(a-b)^2+a^2]t^2\\
&&\quad \quad \quad \quad +\{b(b-a)-1\}^2-a^2
\end{eqnarray*}](images/img740.png)


ゆえに
ここで![]() の複二次式
の複二次式![]() の判別式をとると
の判別式をとると
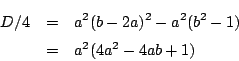
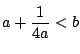 より,
より,![]() である.つまり(2)の条件式は実数解をもたない.
ところが少なくとも一つ
である.つまり(2)の条件式は実数解をもたない.
ところが少なくとも一つ![]() となる点
となる点![]() が存在した.
つまり(2)の条件式に実数解が存在する.
(2)の条件式は4次式で,少なくとも5つの解をもつので恒等的に0で係数はすべて0となり,
が存在した.
つまり(2)の条件式に実数解が存在する.
(2)の条件式は4次式で,少なくとも5つの解をもつので恒等的に0で係数はすべて0となり,
![]() である.
である.
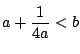 なので
なので![]() である.
である.
このとき任意の点![]() に対して(2)の条件式が成立し,
に対して(2)の条件式が成立し,![]() となる.□
となる.□