![]() に関する2つの二次式
に関する2つの二次式
証明
![]() より,
より,
南海
さて,![]() のときは,
のときは,![]() と
と![]() を考える.
これから
を考える.
これから![]() を消去する.
すると
を消去する.
すると![]() から2回目の操作で定まる点の座標を与える2次方程式が得られるはずだ.
から2回目の操作で定まる点の座標を与える2次方程式が得られるはずだ.
 この2次方程式が重解をもてば,つまり図で
この2次方程式が重解をもてば,つまり図で![]() となれば,確かに4回で閉じる.
それが
となれば,確かに4回で閉じる.
それが![]() を頂点とし,
を頂点とし,![]() に外接し,
に外接し,![]() に内接する四角形が存在するための
に内接する四角形が存在するための![]() に関する必要十分条件になるはずだ.
に関する必要十分条件になるはずだ.
拓生 やってみます.
![]() から
から ![]() を消去し,
を消去し,
![]() の条件の下で
の条件の下で ![]() の関係式を求める.
の関係式を求める.
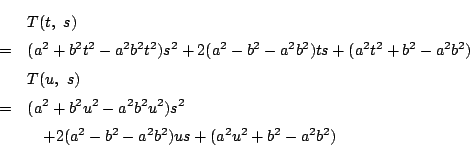
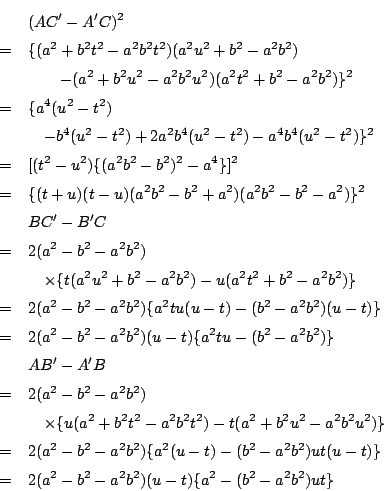
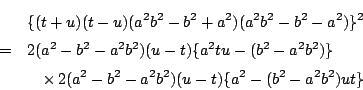

![\begin{eqnarray*}
&& (t+u)^2(a^2-b^2+a^2b^2)^2(a^2+b^2-a^2b^2)^2 \\
&=&4(a^2-...
...^2(b^2-a^2b^2)t^2u^2+\{a^4+(b^2-a^2b^2)^2\}ut
-a^2(b^2-a^2b^2)]
\end{eqnarray*}](images/img860.png)
さて,![]() を一つの頂点とし,
を一つの頂点とし, ![]() に外接しかつ
に外接しかつ ![]() に内接する四辺形がつくられるための
条件は, 今求めた等式を
に内接する四辺形がつくられるための
条件は, 今求めた等式を![]() に関する二次方程式と見たとき,
に関する二次方程式と見たとき,![]() がただ一つだけ存在することである.
そこで, この等式を
がただ一つだけ存在することである.
そこで, この等式を ![]() について整理する.
について整理する.
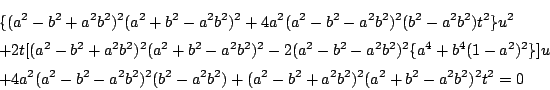
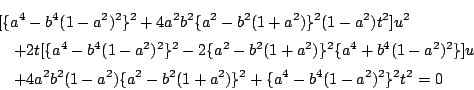
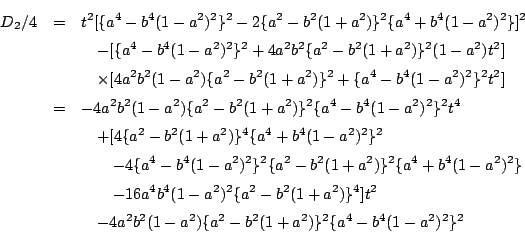
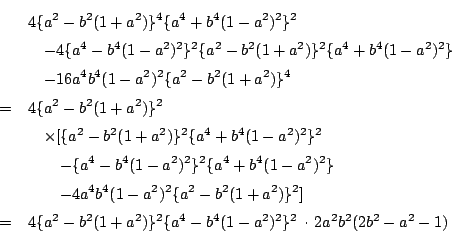

拓生
![]() が
が![]() が満たすべき条件式です.
が満たすべき条件式です.
そこで,

ここで  の二次式
の二次式

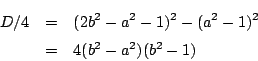
![]() なので,
なので,![]() なら
なら![]() である.
である.
![]() のとき,
のとき,![]() を
を![]() の二次式と見たときの軸は
の二次式と見たときの軸は
よってもし![]() となる
となる![]() が1点でも存在すれば,
が1点でも存在すれば, ![]() が恒等的に0とならねばならない.
が恒等的に0とならねばならない.
このとき任意の![]() に対して
に対して![]() を頂点とする四辺形が存在する.
よって, 求める条件は,
を頂点とする四辺形が存在する.
よって, 求める条件は,
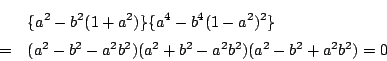
南海 ここで得られた条件は,東大の問題の結果と同じだ.