次： 二次曲線の閉形定理 上： 円の場合を一般的に考える 前： 根軸について

円の場合の一般的証明

南海　 「ポンスレの閉形定理」に生かすために，この補題を次のようにいいかえよう．

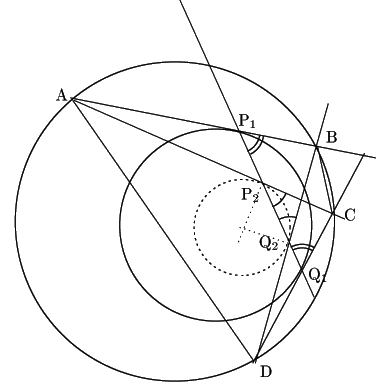
円に内接する四辺形 $\mathrm{ABCD}$ の対辺 $\mathrm{AB},\ \mathrm{CD}$ が一つの円に接するとき， その接点 $\mathrm{P}_1,\ \mathrm{Q_1}$ を結ぶ直線が線分 $\mathrm{AC},\ \mathrm{BD}$ と交わる点を $\mathrm{P}_2,\ \mathrm{Q_2}$とすれば，この点で $\mathrm{AC},\ \mathrm{BD}$に接する円が存在し， かつこの円は他の二円と根軸を共有する．

$\mathrm{P}_2,\ \mathrm{Q_2}$ から $\mathrm{AC},\ \mathrm{BD}$に垂線を引きその交点を中心にして， $\mathrm{P}_2$をとおる円を描けばそれは$\mathrm{Q_2}$ も通り，題意をみたす．

これから次のポンスレの閉形定理が得られる．

定理 10 (ポンスレの定理)

    与えられた円 $O$ に内接する $n$ 角形 $\mathrm{A_1A_2\cdots A_n}$ がある． 辺 $\mathrm{A_1A_2},\ \cdots,\ \mathrm{A_{n-1}A_n}$ はそれぞれ円 $O$ と根軸共有な 定円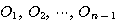に接している．

他の $n$ 角形 $\mathrm{B_1B_2\cdots B_n}$ も 辺 $\mathrm{B_1B_2},\ \cdots,\ \mathrm{B_{n-1}B_n}$ がそれぞれ同じ定円 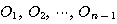に接している．

このとき残る辺 $\mathrm{A_nA_1}$と辺 $\mathrm{B_nB_1}$は円$O$と根軸共有な同一の 定円 $O_n$ に接している．

証明

円 $O$ に内接する四辺形 $\mathrm{A_1A_2B_1B_2}$ において辺 $\mathrm{A_1A_2}$と 辺 $\mathrm{B_1B_2}$は同一の定円 $O_1$ に接するから， $\mathrm{A_1B_1}$ , $\mathrm{A_2B_2}$ も $O,\ O_1$と根軸を共有する一つの円 $C$ に接する．

同様に $\mathrm{A_2B_2}$ , $\mathrm{A_3B_3}$ も $O,\ O_2$と根軸を共有する一つの円 Dに接する．

円D は $\mathrm{A_2B_2}$ に接し，しかも $O,\ O_2,\ O_3$ と根軸を共有する．

ゆえに $C=D$ である．

こうして辺 $\mathrm{A_1B_1},\ \mathrm{A_2B_2},\ \cdots,\ \mathrm{A_nB_n}$ は同じ円 C に接する．

四辺形 $\mathrm{A_1B_1A_nB_n}$ は円 $O$ に内接し，辺 $\mathrm{A_1B_1}$ と辺 $\mathrm{A_nB_n}$ は円 $O$ と根軸を共有する円 $C$ と接する．ゆえに $\mathrm{A_1A_n}$と $\mathrm{B_1B_n}$ も円 $O,\ C$ と根軸を共有する一定の円に接する．□

この定理の特別な場合として

定理 11 (二円の場合の閉形定理)

     一つの定円 $C_1$ に内接し，他の一つの定円 $C_2$ に外接する $n$ 角形 $\mathrm{A_1A_2\cdots A_n}$ がが一つ存在するとする． このとき$C_1$ 上の一点 $\mathrm{P_1}$ から $C_2$ にひとつの接線をひき， その延長が再び $C_1$ と交わる点を $\mathrm{P_2}$ とする． $\mathrm{P_2}$ から $C_2$ に $\mathrm{P_1P_2}$ とは異なる接線をひき，その延長が再び $C_1$ と交わる点を $\mathrm{P_3}$ とする． 以下同様に，順次 $\mathrm{P_4},\ \cdots,\ \mathrm{P_{n+1}}$ を定めると， $\mathrm{P_{n+1}}=\mathrm{P_1}$ となる．

証明 これは $O_1=O_2=\cdots =O_{n-1}=O_n=C_2$としてポンスレの定理を用い， $\mathrm{P_nP_1}$ も $C_2$ に接するので， $\mathrm{P_{n+1}}=\mathrm{P_1}$ となりこれも $n$ 角形になる．□