 二つの二次曲線の位置関係はもちろんいろいろあり得る.
二つの二次曲線の位置関係はもちろんいろいろあり得る.
次のようなときにもポンスレの閉形定理を考えることができるのではないか.
拓生
![]() 上の
点
上の
点![]() から
から![]() に接線を引き,
接線上にある
に接線を引き,
接線上にある![]() の上のもう一つの点を
の上のもう一つの点を![]() とする.
とする.
点![]() から
から![]() に接線を引き,
接線上にある
に接線を引き,
接線上にある![]() の上のもう一つの点を
の上のもう一つの点を![]() とする.
とする.
点![]() から
から![]() に接線を引き,
接線上にある
に接線を引き,
接線上にある![]() の上のもう一つの点を
の上のもう一つの点を![]() とする.….
とする.….
これを繰りかえして,元の![]() に戻ってくるかということですね.
に戻ってくるかということですね.
ある点![]() からはじめて
からはじめて![]() 回で元に戻れば,どこからはじめても元に戻るか.
回で元に戻れば,どこからはじめても元に戻るか.
確かにこのように考えれば,位置関係は自由です.
南海
しかし,このような場合,![]() と
と![]() の両方に接する接線が存在しうる.
の両方に接する接線が存在しうる.
拓生
その場合,![]() の方の点を
の方の点を![]() とすると
とすると
南海 共通接線は何本あるのだろう.
拓生 4本,3本,2本,なし,のいろいろあります.
南海
そこで先に考えた円と円で![]() の場合の例をもう一度考えよう.
の場合の例をもう一度考えよう.
![\begin{eqnarray*}
H(t)&=&<(r-a)\{(r+a)^2-t^2-1\}+(r+a)[\{(r-a)^2-1\}t^2-1]>^2\\
&&\quad \quad -\{(r+a)^2+(r-a)^2t^2\}^2
\end{eqnarray*}](images/img782.png)
そこで,共通接線との関連を調べよう.
![]() 上の点
上の点
![]() が
が
拓生
接線の式は
これが![]() とも接すればよいので
とも接すればよいので
ここで
![]() なので,条件は
なので,条件は
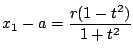 を代入する.
を代入する.

これは定数倍を除くと![]() と同じ式だ.
と同じ式だ.
![]() は共通接線を与える式なのか.でもそれが虚根ということは?
は共通接線を与える式なのか.でもそれが虚根ということは?
南海
拓生
共通接線を![]() とおきます.両方と接するので
とおきます.両方と接するので
 .また
.また .
.
だから接線は
 (第一,第三複号同順)
(第一,第三複号同順)
南海
しかし,それぞれの円の式と連立させて共通根を求めれば,それが重根になることはまちがいない.
もちろん点と直線の距離の式は使えないが,![]() か
か![]() を消去して得られる二次式の判別式をとれば,
距離の式から得られる式と同じ式が得られる.つまり虚根も考えれば,
上の接線の式は
を消去して得られる二次式の判別式をとれば,
距離の式から得られる式と同じ式が得られる.つまり虚根も考えれば,
上の接線の式は![]() の双方と重根をもつ.
そういう意味ではもとの二つの二次曲線とそれぞれ重根をもつ共通接線が4本ある,ということにならないか.
の双方と重根をもつ.
そういう意味ではもとの二つの二次曲線とそれぞれ重根をもつ共通接線が4本ある,ということにならないか.
そしてその共通接線を与える方程式が![]() と一致した.
と一致した.
拓生
それで思い出したのですが,円と二次曲線のいくつかの実例では,
すべて最後に点![]() を媒介変数表示したときの変数
を媒介変数表示したときの変数![]() についての四次方程式が得られました.
そしてそれが恒等的に0になることを示そうとしました.
についての四次方程式が得られました.
そしてそれが恒等的に0になることを示そうとしました.
恒等的に0になるためには,実根でなくても虚根を含めて, しかも重根の場合は重複度も含めて,次数より1多い根があればそれで恒等的に0になるのでした. 図形から出発したので実数解ばかり考えますが,恒等式かどうかの判断は実数でなくてもよい.
南海 そうだ.あわせて考えをまとめると
拓生 これはポンスレの閉形定理の証明になっていますね.
南海
念のため,その他の場合も![]() の根と共通接線の関係を確認しておいてほしい.
の根と共通接線の関係を確認しておいてほしい.
拓生

![]() なら
なら![]() の解は一つ.
の解は一つ.
![]() の解が二つになるのは,
の解が二つになるのは,
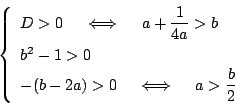
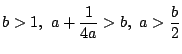 のときで,
位置関係はそれぞれ図のようになり,共通接線はそれぞれ2本,4本,4本である.
のときで,
位置関係はそれぞれ図のようになり,共通接線はそれぞれ2本,4本,4本である.
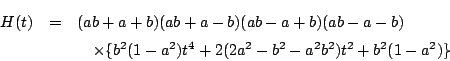
共通接線の交点の方程式は求めていませんが,![]() が実根をもつ場合と
共通接線が存在する場合との同値性から,同じ式になることもまちがいありません.
が実根をもつ場合と
共通接線が存在する場合との同値性から,同じ式になることもまちがいありません.
南海 式は求めればできるが,求めなくても一致することはまちがいない.それでいいでしょう.