次： フェルマ点証明の解析的方法 上： フェルマ点 前： トレミーの定理

フェルマ点

定理 2 (フェルマ点)

    三角形 $\mathrm{ABC}$ と，三辺の比が

$$\mathrm{L_2L_3}:\mathrm{L_3L_1}:\mathrm{L_1L_2}=r_1:r_2:r_3$$

である三角形 $\mathrm{L_1L_2L_3}$ がある．

点 $\mathrm{P_1,\,P_2,\,P_3}$ を

$$\bigtriangleup \mathrm{L_1L_2L_3} \propto \bigtriangleup \ma... ...iangleup \mathrm{AP_2C} \propto \bigtriangleup \mathrm{ABP_3}$$

であるようにとる． $ \angle \mathrm{BAC}+\angle \mathrm{CAP_2}< 180^{\circ} $ ， $ \angle \mathrm{ABC}+\angle \mathrm{CBP_1}< 180^{\circ} $ であるとする． このとき，

1. 三直線 AP₁ ，BP₂ ，CP₃は一点 $\mathrm{P}$ で交わる．
2. $\mathrm{P}$ は
   
   $$r_1 \mathrm{AP}+ r_2 \mathrm{BP}+ r_3 \mathrm{CP}$$
   を最小にする点である．

拓生　 証明をやってみます．

証明

1. $\mathrm{AP_1}$ と $\mathrm{BP_2}$ の交点を $\mathrm{P}$ とする．
   
   $$\mathrm{AC}:\mathrm{CP_2} =\mathrm{P_1C}:\mathrm{CB},\, \angle \mathrm{ACP_1}= \angle \mathrm{BCP_2}$$
   
   
   であるから,
   
   $$\bigtriangleup \mathrm{ACP_1} \propto \bigtriangleup \mathrm{BCP_2}$$
   
   
   よって
   
   $$\angle \mathrm{AP_1C}= \angle \mathrm{P_2BC}$$
   
   
   よって点 $\mathrm{B},\ \mathrm{P_1} ,\ \mathrm{C} ,\ \mathrm{P}$ が同一円周上にある． これから
   
   $$\angle \mathrm{P_1CB}= \angle \mathrm{P_1PB}=\angle \mathrm{BP_3A}$$
   
   
   ここで, $\angle \mathrm{BP_3A}+\angle \mathrm{BPA}=180^{\circ}$ より $\mathrm{P} ,\ \mathrm{A} ,\ \mathrm{P_3} ,\ \mathrm{B}$ も同一円周上にある．

   よって,
   

   $$\angle \mathrm{APP_3}=\angle \mathrm{ABP_3}$$
   
   
   一方, 点 $\mathrm{B},\ \mathrm{P_1} ,\ \mathrm{C} ,\ \mathrm{P}$ が同一円周上にあるので
   
   $$\angle \mathrm{P_1BC}=\angle \mathrm{P_1PC}$$
   
   
   よって対頂角が等しいので, $\mathrm{P_3},\ \mathrm{P},\ \mathrm{C}$ が同一直線上にある．

   つまり, 三直線 $\mathrm{AP1},\ \mathrm{BP_2},\ \mathrm{CP_3}$ は一点 $\mathrm{P}$ で交わる．

2. トレミーの定理より,
   
   $$\mathrm{AP}\cdot\mathrm{BP_3}+\mathrm{BP}\cdot\mathrm{AP_3} =\mathrm{AB}\cdot\mathrm{P_3P}$$
   
   
   つまり
   
   $$r_1\mathrm{AP}+r_2\mathrm{BP}=r_3\mathrm{P_3P}$$
   
   
   よって,
   
   $$r_1 \mathrm{AP}+ r_2 \mathrm{BP}+ r_3 \mathrm{CP}=r_3 \mathrm{P_3C} (一定)$$
   
   
   他の $\mathrm{P}$ に対してはトレミーの定理より,
   
   $$\mathrm{AP}\cdot\mathrm{BP_3}+\mathrm{BP}\cdot\mathrm{AP_3} >\mathrm{AB}\cdot\mathrm{P_3P}$$
   
   
   となるので,
   
   $$r_1 \mathrm{AP}+ r_2 \mathrm{BP}+ r_3 \mathrm{CP}>r_3 \mathrm{P_3C} (一定)$$
   
   
   である．つまり $\mathrm{P}$ は
   
   $$r_1 \mathrm{AP}+ r_2 \mathrm{BP}+ r_3 \mathrm{CP}$$
   
   
   を最小にする点である．□

南海　 よくできている．ただ，三角形の頂角が $ 120^{\circ} $より小さいという条件がいる．

拓生　 はじめの質問の点は, $\mathrm{L_2L_3}:\mathrm{L_3L_1}:\mathrm{L_1L_2}=1:1:1$ である正三角形 $\mathrm{L_1L_2L_3}$ をとればいいのですね．

南海　そう．
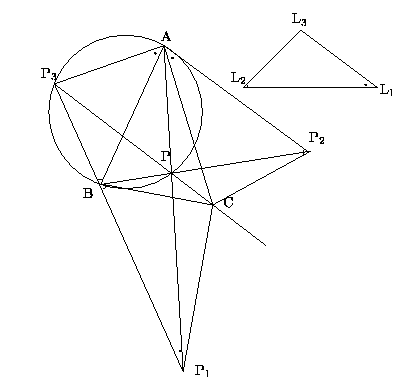
このとき， $ \bigtriangleup \mathrm{ABC} $ の外に正三角形 $ \bigtriangleup \mathrm{P_1BC} $ ， $ \bigtriangleup \mathrm{AP_2C} $ ， $ \bigtriangleup \mathrm{ABP_3} $ をとる． 三直線 $ \mathrm{AP_1}，\mathrm{BP_2}，\mathrm{CP_3} $ の交点 $ \mathrm{P} $ が求める点だ． この点を $ \bigtriangleup \mathrm{ABC} $ のフェルマ点という． \[ \angle \mathrm{APB}=180^{\circ}-\angle \mathrm{BS_3A}=120^{\circ} \] 三角形 $ \mathrm{AP_3C} $ と 三角形 $ \mathrm{ABP_2} $ は合同なので， $ \mathrm{P_3C} $ と $ \mathrm{P_2B} $ の交点を $ \mathrm{W} $ とすると， $ \mathrm{P_3},\ \mathrm{B},\ \mathrm{W},\ \mathrm{A} $ は同一円周上にあり， $ \mathrm{A},\ \mathrm{W},\ \mathrm{C},\ \mathrm{P_2} $ も同一円周上にある．

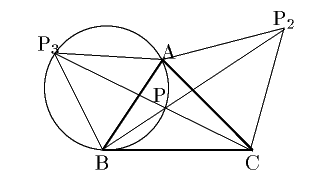
この結果 $ \mathrm{W} $ は2つの外接円の交点であり， $ \mathrm{P_3},\ \mathrm{P},\ \mathrm{W} $ は同一直線上にあるので， $ \mathrm{P}=\mathrm{W} $ となる．この結果， \[ \angle \mathrm{APC}=120^{\circ} \] となり， \[ \angle \mathrm{APC}=\angle \mathrm{BPA}=\angle \mathrm{CPB}=120^{\circ} \] である．
$ \angle \mathrm{BAC} >120^{\circ} $ のとき \[ \angle \mathrm{P_3AB}+\angle \mathrm{BAC} >180^{\circ} \] となり，交点 $ \mathrm{P} $ は存在しない．
このとき， $ \mathrm{AP}+\mathrm{BP}+\mathrm{CP} $ を最小にする点は $ \mathrm{A} $ であることを示す．
点 $ \mathrm{B},\ \mathrm{C} $ をとおりこれに直交する2つの直線と 頂点 $ \mathrm{A} $ の外角の2等分線でできる三角形を $ \mathrm{A'B'C'} $ とする． 任意の点 $ \mathrm{P} $ からこれらの辺に下ろした垂線の足を $ \mathrm{A"B"C"} $ とする．

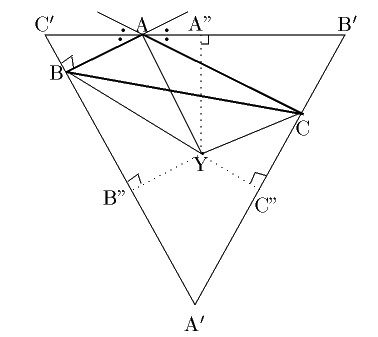
このとき， \[ \angle \mathrm{A'}< 60^{\circ},\quad \angle \mathrm{B'}=\angle \mathrm{C'} >60^{\circ} \] そして， \[ \mathrm{A'B'}=\mathrm{A'C'} >\mathrm{B'C'} \] である． \[ \mathrm{AP}+\mathrm{BP}+\mathrm{CP} >\mathrm{A"P}+\mathrm{B"P}+\mathrm{C"P} \] であるが，面積を考えることで， \begin{eqnarray*} &&\left(\mathrm{AP}+\mathrm{BP}+\mathrm{CP} \right)\cdot\mathrm{A'B'}\\ &\geqq&2\bigtriangleup \mathrm{A'B'C'} =(\mathrm{AB}+\mathrm{AC})\cdot\mathrm{A'B'} \end{eqnarray*} であるから， \[ \mathrm{A"P}+\mathrm{B"P}+\mathrm{C"P}\geqq \mathrm{AB}+\mathrm{AC} \] この結果， \[ \mathrm{AP}+\mathrm{BP}+\mathrm{CP}\geqq\mathrm{AB}+\mathrm{AC} \] となり， 点 $ \mathrm{P} $ を $ \mathrm{A} $ にとったとき，最小となる．