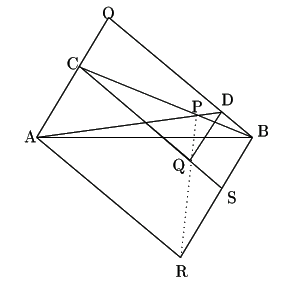
 解答
解答
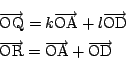
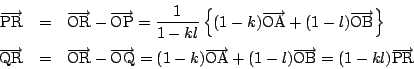
よって
![]() と
と
![]() が平行となり,
3点
が平行となり,
3点
![]() は一直線上にある.
□
は一直線上にある.
□
これはベクトルの威力がわかる証明です.
質問は2点あって,
南海 うん,このようなことを考えるのは大変いいことだ.
まず図形的な証明だが.メネラウスの定理を使えばできる.
念のためにメネラウスの定理を示しておこう.
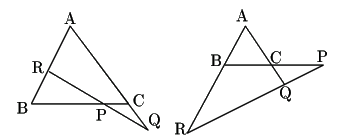 3点
3点
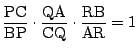 となる.
となる.
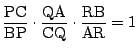 なら
3点
なら
3点
(1)をメネラウスの定理といい,
(2)をメネラウスの定理の逆という.
要するに条件
証明
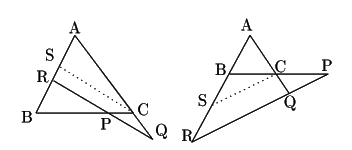 (1)
点
(1)
点![]() から
から
![]() に平行な
直線
に平行な
直線![]() を引く.
を引く.
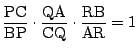 なので
なので
南海 これを用いて先の演習問題の図形的な証明を考えよう.
![]() と
と![]() の交点を
の交点を![]() とおこう.
これを先の図に書き込む.
とおこう.
これを先の図に書き込む.
方針は,
![]() と,
辺または辺の延長上の3点
と,
辺または辺の延長上の3点
![]() に
関して,メネラウスの定理の逆を用いて,
この3点が一直線上にあることをいいたい.
に
関して,メネラウスの定理の逆を用いて,
この3点が一直線上にあることをいいたい.
伍郎
そのためには,
南海
![]() と直線
と直線![]() に関してメネラウスの定理を用いると何が得られるか.
に関してメネラウスの定理を用いると何が得られるか.
伍郎
わかりました.意外に簡単なのですね.