![]() を射影座標とする.このとき,
を射影座標とする.このとき,
もちろん,普通の平面の場合と同様,これが因数分解されて二つの直線などになる場合もある.
このとき,曲線上の点
![]() に対して
に対して
この接線を『パスカルの定理』では微分で考えたので, ここでは少し違う形で考えよう.
![]() のとき,
のとき,
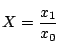 ,
,
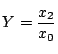 とおくと,曲線
とおくと,曲線![]() の方程式は
の方程式は
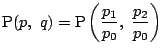 となるものとする.
となるものとする.
![]() を通る直線の方向が
を通る直線の方向が
![]() のものを,
媒介変数
のものを,
媒介変数![]() を用いて
を用いて
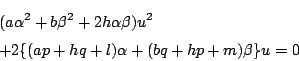
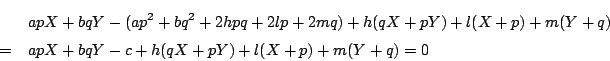
ここに,
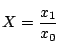 ,
,
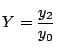 ,
,
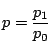 ,
,
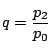 を代入して分母を払うと
先の
を代入して分母を払うと
先の![]() の方程式が得られる.
の方程式が得られる.
伍郎
いちいち
![]() で書くのは大変ですね.
で書くのは大変ですね.
南海
そこで,
![]() とし,
とし,
![]() の式を
の式を![]() と書こう.
また接線の式を
と書こう.
また接線の式を![]() とおくのだった.
とおくのだった.
伍郎
『パスカルの定理』にあるように![]() は
は![]() と
と![]() に関して対称で,
に関して対称で,
 定理 4 (極と極線)
定理 4 (極と極線)
![]() から二本の接線を引く.接点を
から二本の接線を引く.接点を![]() とする.
直線
とする.
直線![]() 上の任意の点
上の任意の点 ![]() をとる.
をとる.
![]() から二本の接線を引く.
接点を
から二本の接線を引く.
接点を![]() とする.
とする.
すると 直線![]() は
は![]() を通る.
を通る.
証明
接点の座標をそれぞれ,![]() とする.接線の方程式は
とする.接線の方程式は
点 ![]() のことを極,
直線
のことを極,
直線![]() のことを極線といいます.
のことを極線といいます.
南海
さて.パスカルの定理だ.
 定理 5 (パスカルの定理)
定理 5 (パスカルの定理)
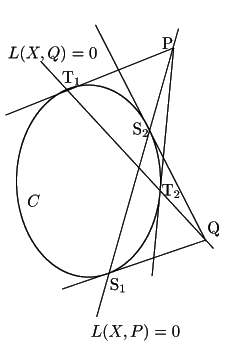
2次の斉次式で定まる曲線![]() の上に異なる6点
の上に異なる6点
![]() と
と
![]() を取る.
を取る.
直線
![]() と直線
と直線
![]() の交点を
の交点を![]() ,
直線
,
直線
![]() と直線
と直線
![]() の交点を
の交点を![]() ,
直線
,
直線
![]() と直線
と直線
![]() の交点を
の交点を![]() とする.
とする.
このとき3点
![]() は一直線上にある.
は一直線上にある.
南海 この証明のために,補題が必要だ.
補題 1
![]() 上に,任意の5点を与えるとき,
これらすべてを通る2次曲線
上に,任意の5点を与えるとき,
これらすべてを通る2次曲線![]() が存在する.
これらの5点のうち,少なくとも4点が1直線上にないかぎり,
が存在する.
これらの5点のうち,少なくとも4点が1直線上にないかぎり,
![]() はただ一つに定まる.
はただ一つに定まる.
この証明は代数的な準備が必要で,ここでは出来ない. 参考文献『代数曲線の幾何学』などを見てほしい. 2次の斉次式は6個の定数でできているが, 5個の通る点が与えられれば,係数の比が定まるところまでは, 何とかいけるが,一意性の証明はもう少し準備がいる.
それを今後の勉強の課題としておいて,パスカルの定理を証明しよう.
証明
点![]() での接線と
での接線と![]() での接線の交点を
での接線の交点を
![]() とかくと,
直線
とかくと,
直線
![]() は
は
以下同様に記号を定める.
そこで,次の二次式を満たす曲線
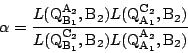
補題1から,![]() と
と![]() は同一の曲線となる.
は同一の曲線となる.
同様に次の二次式を満たす曲線
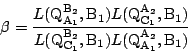
二つの二次曲線の式は定数倍を除いて一致する.
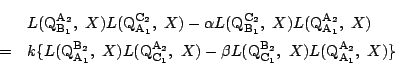
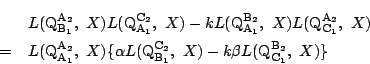
左辺に
![]() を代入すると0になるので,右辺も満たす.
そして
を代入すると0になるので,右辺も満たす.
そして
![]() は
は
![]() 上にはない.よって,
上にはない.よって,
ここで,
![]() と置くとこの式は
と置くとこの式は
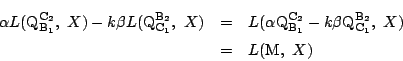
伍郎 これでパップスの定理も示せているのですか.
実はこの2次曲線は既約でなくてもいいのだ.だから![]() として
として
![]() と
と![]() の方程式の積で定まる曲線でいいのだ.
そのことをはっきりさせるために,
パップスの定理型に再編してみてほしい.
の方程式の積で定まる曲線でいいのだ.
そのことをはっきりさせるために,
パップスの定理型に再編してみてほしい.
伍郎
直線![]() の方程式を
の方程式を![]() とし,
2次式
とし,
2次式![]() を考える.
を考える.
![]() を通る直線の方程式を
を通る直線の方程式を![]() とする.
以下同様に次のように定める.
とする.
以下同様に次のように定める.
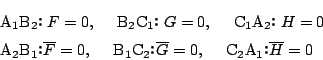
したがって式
![]() と式
と式
![]() に
に
![]() の座標を代入したものの比を
の座標を代入したものの比を![]() とすると,
方程式
とすると,
方程式
ところが
![]() のこの5点を通るので,補題1から
2つの2次式
のこの5点を通るので,補題1から
2つの2次式
![]() と
と![]() は定数倍しか違わない.
は定数倍しか違わない.
同様に![]() ,
,![]() は
は
![]() ,
,
![]() を通る.定数
を通る.定数![]() を選ぶと
を選ぶと
よって
2つの2次式
![]() と
と
![]() は定数倍しか違わない.
は定数倍しか違わない.
![]() の各1次式にその定数をかけ,
それを改めてその1次式にとりなおすことで,
2つの2次式
の各1次式にその定数をかけ,
それを改めてその1次式にとりなおすことで,
2つの2次式
![]() と
と
![]() は一致するようにできる.
は一致するようにできる.
この2点は![]() は満たさない.よってこの2点は
1次方程式
は満たさない.よってこの2点は
1次方程式