次: パップスの定理はパスカルの定理の特別な場合 上: パップスの定理 前: 射影変換

射影幾何的証明

伍郎　 3直線が1点交わるとか，いうことは射影変換しても変わらないから， 適当な射影変換で移して示しても一般性は失われないのですね．

南海　 そういうことなのだ． そこで，パップスの定理を射影幾何的に証明してみよう．

2つの直線$l_1$と$l_2$のうち一方を無限直線と見なすのだ． この場合に示せれば，適当な射影変換をして， 無限遠からこちらにもってくれば一般の場合に成立することがわかる．

伍郎　 待ってください．無限直線上で交わるということは，実は平行ということなのだから，$l_2$を無限直線とすれば，

$$\mathrm{A}_1\mathrm{B}_2 \parallel \mathrm{C}_1\mathrm{B}_2,... ...\mathrm{A}_1\mathrm{C}_2 \parallel \mathrm{C}_1\mathrm{C}_2,\$$

のもとで示せばよいのですか．

南海　 実はそうなのだ．

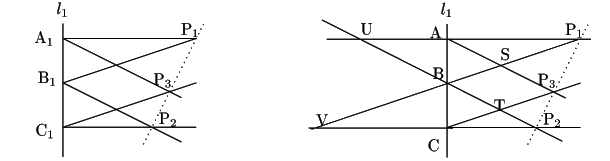
伍郎　 この左図ではどう考えればよいのでしょうか．

南海　 右のように延長して交点に名前をつけよう．

$\bigtriangleup \mathrm{P_1VP_2}$に注目して，

$$\mathrm{P}_1\mathrm{B}：\mathrm{P}_1\mathrm{S}= \mathrm{P}_2\mathrm{B}：\mathrm{S}\mathrm{P}_3$$

を示せば，平行2直線と比の対応から，$\mathrm{P}_3$ が $\mathrm{P}_1\mathrm{P}_2$上のにあることがわかる．

伍郎　 平行線による比の移動を見ていくと

$$\mathrm{P}_1\mathrm{B}：\mathrm{P}_1\mathrm{S}= \mathrm{P}_1... ...m{B}\mathrm{T}= \mathrm{P}_2\mathrm{B}：\mathrm{S}\mathrm{P}_3$$

です．

しかし，ということは，私のはじめの問題も，あれで実はパップスの定理の一般的な証明だったのではないですか．

南海　 そうなんだ． パップスの定理での，辺と交わる図1.2において， 直線$\mathrm{EF}$を無限直線にした場合なのだ．

あの最初の状態で証明しておいて，直線$\mathrm{EF}$を有限の場所に射影変換で移せば，それが一般の場合のパップスの定理になるのだ．

伍郎　 これって，すごい世界ですね．射影幾何をもっと勉強したくなりました．