放物線![]() 上に相異なる三点,
上に相異なる三点,
![]() ,
,
![]() ,
,
![]() がある.
原点を中心とする半径1の円を
がある.
原点を中心とする半径1の円を![]() とし,
直線
とし,
直線![]() ,直線
,直線![]() はそれぞれ
はそれぞれ![]() に接するとする.
このとき,直線
に接するとする.
このとき,直線![]() もまた
もまた![]() に接することを証明せよ.
に接することを証明せよ.
拓生 最近,三つのよく似た問題に出会いました.まず問題を見て下さい.
放物線![]() 上に相異なる三点,
上に相異なる三点,
![]() ,
,
![]() ,
,
![]() がある.
原点を中心とする半径1の円を
がある.
原点を中心とする半径1の円を![]() とし,
直線
とし,
直線![]() ,直線
,直線![]() はそれぞれ
はそれぞれ![]() に接するとする.
このとき,直線
に接するとする.
このとき,直線![]() もまた
もまた![]() に接することを証明せよ.
に接することを証明せよ.
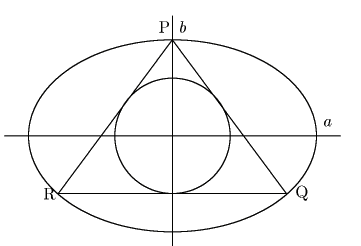
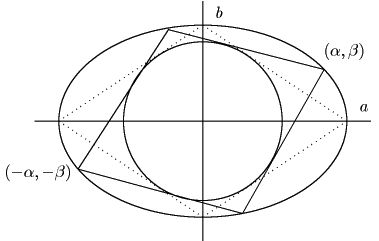
円![]() を内部に含む楕円
を内部に含む楕円
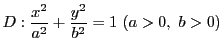 がある.
がある.
![]() 上の一点
上の一点
![]() から
から![]() にひとつの接線をひき,
その延長が再び
にひとつの接線をひき,
その延長が再び![]() と交わる点を
と交わる点を![]() とする.
とする.
![]() から
から![]() に
に![]() とは異なる接線をひき,
その延長が再び
とは異なる接線をひき,
その延長が再び![]() と交わる点を
と交わる点を![]() とする.
とする.
![]() から
から![]() に
に![]() とは異なる接線をひき,
その延長が再び
とは異なる接線をひき,
その延長が再び![]() と交わる点を
と交わる点を![]() とすると
とすると![]() となった.
このとき
となった.
このとき![]() を
を![]() の関数として表わせ.
の関数として表わせ.
円![]() を
を![]() ,
楕円
,
楕円
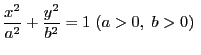 を
を![]() とする.
とする.
![]() 上のどんな点
上のどんな点![]() に対しても,
に対しても,![]() を頂点にもち,
を頂点にもち,
![]() に外接して
に外接して![]() に内接する平行四辺形が存在するための必要十分条件を
に内接する平行四辺形が存在するための必要十分条件を
![]() で表せ.
で表せ.
南海 とりあえず三つの問題自身はできたか.
拓生 はい.名古屋大,京大の問題は難しくありません.東大のも何とかなりました.
南海 拓生君は次のような解答を示した.
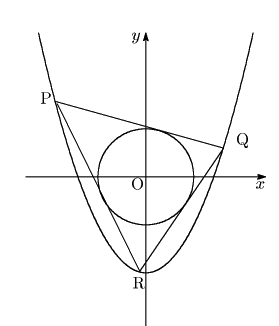 例題1.1解答
例題1.1解答
直線![]() の式は,
の式は,
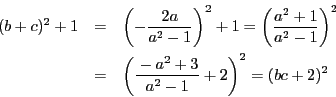
 例題1.2解答
例題1.2解答
![]() となるということは,
となるということは,![]() から円に二つの接線を引き,楕円との交点
を
から円に二つの接線を引き,楕円との交点
を![]() ,
,![]() とするとき,直線
とするとき,直線![]() が再び円に接する,ということである.
が再び円に接する,ということである.
![]() が
が![]() 軸上の点であり,円も楕円も
軸上の点であり,円も楕円も![]() 軸対称の位置にあるので,
直線
軸対称の位置にあるので,
直線![]() が再び円に接するのは,
が再び円に接するのは,![]() と
と![]() の
の![]() 座標が
座標が![]() のときである.
のときである.
従って題意をみたす![]() と
と![]() はあるとすれば一組のみであるから,
はあるとすれば一組のみであるから,
![]() と
と![]() をその
をその![]() 座標が -1 の楕円上の点とするとき,
座標が -1 の楕円上の点とするとき,
![]() が円と接することが
が円と接することが
![]() となるための条件である.
となるための条件である.
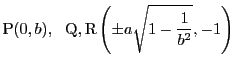 である.
である.
![]() の式は,
の式は,
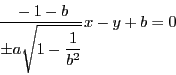
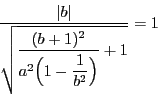
 例題1.3解答
例題1.3解答
[必要条件]
![]() を
を![]() とし,
とし,
![]() とする.
とする.
![]() を頂点の一つとする平行四辺形が存在するためには,円と楕円がともに
を頂点の一つとする平行四辺形が存在するためには,円と楕円がともに![]() 軸,
軸,
![]() 軸に関して対称であるから,
軸に関して対称であるから,![]() が円に接しなければならない.
が円に接しなければならない.
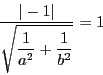
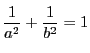 のとき,題意をみたす平行四辺形が存在することを示せばよい.
のとき,題意をみたす平行四辺形が存在することを示せばよい.
交点は
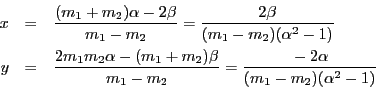
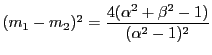 に注意して,
この交点を楕円の式に代入する.
に注意して,
この交点を楕円の式に代入する.
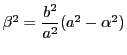 であるから,これを代入して整理すると,
であるから,これを代入して整理すると,
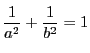 は十分条件である.□
は十分条件である.□
南海 東大の問題は,円に外接する平行四辺形は菱形であること使えばもっと簡単にできる.しかしそれは受験数学的な方法でポンスレの定理に対する個別の対応になる. 上のように一般的に考えて解くことは大切なことだ.
拓生
![]() と順にとって
と順にとって
![]() になるのと,
になるのと,
![]() から二つの接線
から二つの接線![]() と
と![]() を引いたとき,
を引いたとき,
![]() もまた円に接することとは同値です.
それは,外部の点から円への接線がちょうど2本引けることからわかります.
もまた円に接することとは同値です.
それは,外部の点から円への接線がちょうど2本引けることからわかります.
そこで,京大の問題は,
![]() を特別な点としたとき
を特別な点としたとき![]() となる条件を求めよというものです.
一方,名大の問題は三点が一般的に文字で与えられているのですから,
となる条件を求めよというものです.
一方,名大の問題は三点が一般的に文字で与えられているのですから,![]() を
どこにとっても,
を
どこにとっても,![]() となるというのです.
また東大の問題は4点について,二つの問題の中間を主張していて,平行四辺形という条件
にしぼれば,常に同様のことが成り立つ,と主張しています.ある4点を頂点とする平行四辺形が存在することから必要条件を求め,
そのときつねに指定された点を頂点とする平行四辺形が存在
することを示すのですから.
となるというのです.
また東大の問題は4点について,二つの問題の中間を主張していて,平行四辺形という条件
にしぼれば,常に同様のことが成り立つ,と主張しています.ある4点を頂点とする平行四辺形が存在することから必要条件を求め,
そのときつねに指定された点を頂点とする平行四辺形が存在
することを示すのですから.
それぞれ類似のことを証明させようとしていますが,また同時に少しずつ違っていて, どのようなことが成り立つのか,背景にどのような事実があるのか,はっきりわかりません.
南海 問題とされていることがそれぞれ違うのは,入試問題としての難易を調節するためである. こういうときにいちばんいいのは,「できるだけ一般的にとらえ,具体的に考える」ことだ.
拓生 東大の問題も必ずしも平行四辺形でなくても四辺形で成り立つ,のですか.
南海 いや,東大の問題では次のことに注意すれば結局は菱形しかないことがわかる.
同心の円と楕円があり,円が楕円の内部にあるとする. 円に外接し楕円に内接する四角形は結局のところ平行四辺形しかない.円に外接する四角形の隣りあう辺の長さは等しい.一方円も楕円も原点に関して対称なので, 必ずひし形になる.
拓生 なるほど.すると一般に,
円と二次曲線で,ある点が成り立つということでしょうか.から順に接線を引いて,3回目 (ないしは4回目)の点
について
になれば,
をどこにとっても常に
となる.
南海 その通り. 放物線と楕円が出てきたので,そこを「二次曲線」ととらえたのも大変よろしい.
南海
しかしさらに一般化すれば,中の円も「二次曲線」にしたくなる.
また,3および4で成り立つのだから,これを一般に![]() にしたくなる.
二つの二次曲線が置かれた位置関係も制限が必要ない.
一般に二つの二次曲線
にしたくなる.
二つの二次曲線が置かれた位置関係も制限が必要ない.
一般に二つの二次曲線![]() と3以上の自然数
と3以上の自然数![]() に関して,
に関して,
ことが成り立つと推測される. これは,ポンスレの閉形定理, あるいは略してポンスレの定理とよばれている. 一般の場合,複素射影幾何の場で証明される.これは後に考えたい. まず,上の三つの入試問題をそれぞれ一般的に考えよう.上のある点を頂点の一つとし,
に外接し
に内接する
角形が少なくとも一つ存在すれば, 任意の点についてそれを頂点の一つとする同様の
角形が存在する.