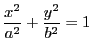 で
で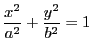 で
で
![]() を円
を円![]() とし,
とし,![]() を放物線
を放物線![]() を考える.
ここで定数は条件
を考える.
ここで定数は条件
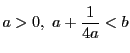 を満たしているとする.
を満たしているとする.
![]() 座標が
座標が![]() と異なる
と異なる![]() 上の点
上の点
![]() から
から![]() にひとつの接線をひき,
その延長が再び
にひとつの接線をひき,
その延長が再び![]() と交わる点を
と交わる点を
![]() とする.
とする.
![]() から
から![]() に
に![]() とは異なる接線をひき,
その延長が再び
とは異なる接線をひき,
その延長が再び![]() と交わる点を
と交わる点を![]() とする.
とする.
![]() から
から![]() に
に![]() とは異なる接線をひき,
その延長が再び
とは異なる接線をひき,
その延長が再び![]() と交わる点を
と交わる点を![]() とする.
とする.
拓生 やってみます.
解答
(1)
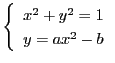 において
において![]() を消去する.
を消去する.
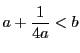 のときは
のときは
![]() とする.直線
とする.直線![]() の式は
の式は
(2)
点
![]() とする.
とする.
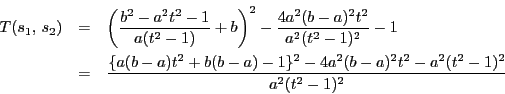
対称性から![]() となるために点
となるために点![]() の
の![]() 座標は1でなければならない.
座標は1でなければならない.
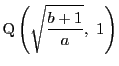 とする.
直線
とする.
直線![]() が円
が円![]() に接すればよい.
に接すればよい.![]() の傾きは
の傾きは
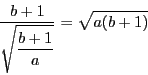
南海 名古屋大学の問題は確かにこの条件を満たしてる.
拓生
はい.
![]() のとき(2)の条件は
のとき(2)の条件は
(4)
(2)の条件式![]() を変形する.
を変形する.
![\begin{eqnarray*}
H(t)&=&a^2\{(b-a)^2-1\}t^4+2[ab(b-a)^2-a(b-a)-2a^2(a-b)^2+a^2]t^2\\
&&+\{b(b-a)-1\}^2-a^2
\end{eqnarray*}](images/img123.gif)
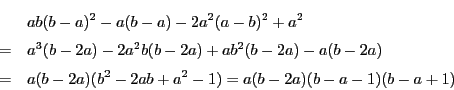
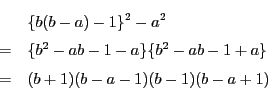
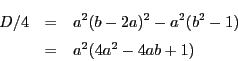
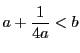 より,
より,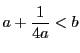 なので
なので
南海 その通り.円と円の場合も次のように考えよう.
![]() は
は![]() を満たす正の定数とする.
を満たす正の定数とする.
![]() 平面の二つの円
平面の二つの円
![]() がある.
がある.
![]() 上の一点
上の一点![]() から
から![]() にひとつの接線をひき,
その延長が再び
にひとつの接線をひき,
その延長が再び![]() と交わる点を
と交わる点を![]() とする.
とする.
![]() から
から![]() に
に![]() とは異なる接線をひき,
その延長が再び
とは異なる接線をひき,
その延長が再び![]() と交わる点を
と交わる点を![]() とする.
とする.
![]() から
から![]() に
に![]() とは異なる接線をひき,
その延長が再び
とは異なる接線をひき,
その延長が再び![]() と交わる点を
と交わる点を![]() とする.
とする.
 と媒介変数表示できることを示せ.また,
と媒介変数表示できることを示せ.また,
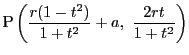 ,
,
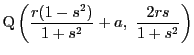 とするとき,直線
とするとき,直線拓生 やってみます.
解答
(1)
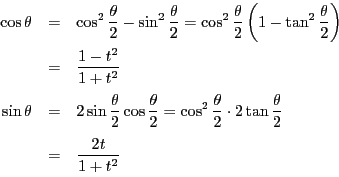
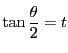 によって
によって
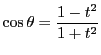 ,
,
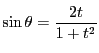 と表される.
すべての実数に対して,
と表される.
すべての実数に対して,
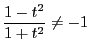 なので,
円
なので,
円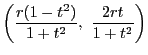 と表される.
と表される.
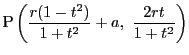 ,
,
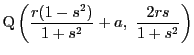 のとき直線
のとき直線![]() の方程式は
の方程式は
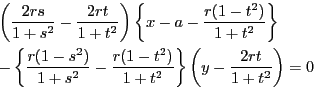
(2)
![\begin{eqnarray*}
T(s,\,t)&=&\{(r-a)st+r+a\}^2-(st-1)^2-(s+t)^2\\
&=&
[\{(r-a)^2-1\}t^2-1]s^2+2(r^2-a^2)ts+(r+a)^2-t^2-1
\end{eqnarray*}](images/img152.gif)
拓生
![]() の係数が0でないことが確認できません.
の係数が0でないことが確認できません.
南海
ここを厳密にやるには,![]() や
や![]() そのものを射影直線上の媒介変数としなければならない.
ここでは,
P,Qが一般の位置にあるとして計算し,そのあと極限をとるという考え方でゆこう.
そのものを射影直線上の媒介変数としなければならない.
ここでは,
P,Qが一般の位置にあるとして計算し,そのあと極限をとるという考え方でゆこう.
拓生
続けます.
![]() を
を![]() の2次方程式と見たときその2解
の2次方程式と見たときその2解![]() は,
は,
![\begin{eqnarray*}
(s_1+s_2)^2+(s_1s_2-1)^2
&=&\dfrac{4(r^2-a^2)^2t^2+\{(r+a)^2...
...\
&=&\dfrac{\{(r+a)^2+(r-a)^2t^2\}^2}{[\{(r-a)^2-1\}t^2-1]^2}
\end{eqnarray*}](images/img157.gif)
![\begin{eqnarray*}
H(t)&=&<(r-a)\{(r+a)^2-t^2-1\}+(r+a)[\{(r-a)^2-1\}t^2-1]>^2\\
&&-\{(r+a)^2+(r-a)^2t^2\}^2
\end{eqnarray*}](images/img158.gif)
(3)
![]() を整理する.
を整理する.
![\begin{eqnarray*}
H(t)&=&
<(r-a)\{(r+a)^2-t^2-1\}+(r+a)[\{(r-a)^2-1\}t^2-1]\\ ...
...&=&\{(r^2-a^2)^2-4r^2\}\{(r-a+1)t^2+r+a+1\}\{(r-a-1)t^2+r+a-1\}
\end{eqnarray*}](images/img160.gif)
南海
これは,ポンスレの定理の起源となる場合である.
拓生
$a$ は外接円と内接円の中心間の距離で,外接円の半径$r$と内接円の半径1の間に成り立つ関係です.
一般的に,外接円の半径を $R$,内接円の半径を $r$ とし,外心,内心を $\mathrm{O},\ \mathrm{I}$ とすると,
\[
\mathrm{OI}^2=R^2-2Rr
\]
が成り立ちます.これは2012年の宮崎大に出題され,
京大でも,2002年,2006年,そして2017年に関連問題が出題,
2018年には東北大学でも出題されています.
チャップルの定理というのではないでしょうか.
南海
チャップルは三角形に内接する円と外接する円の,中心間と半径の相互関係として,
上記定理を導いたのだろう.
しかしこの関係式は円の相互関係のみで記されており,
三角形は関与していない.
拓生
確かにそうです.
南海
ポンスレはこのことから,この関係式を満たす2円に対して,
つねに一方に外接し一方に内接する三角形が存在すること,
そしてさらに,三角形の頂点の一つが任意の選べることに至ったのではないかと思われる.
さらにそれを2つの2次曲線,3に変えて $n$ と一般化していったのではないか.
拓生 そう考えると,これは確かにポンスレの定理の起源になるのですね.
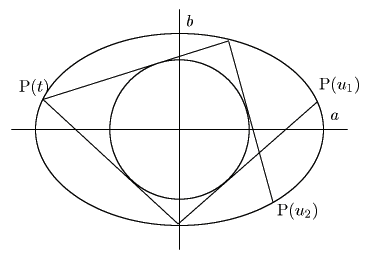
![]() 平面の円と楕円
平面の円と楕円
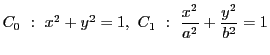 がある.
がある.
定数は条件![]() を満たしているとする.
を満たしているとする.
![]() 上の一点
上の一点![]() から
から![]() にひとつの接線をひき,
その延長が再び
にひとつの接線をひき,
その延長が再び![]() と交わる点を
と交わる点を![]() とする.
とする.
![]() から
から![]() に
に![]() とは異なる接線をひき,
その延長が再び
とは異なる接線をひき,
その延長が再び![]() と交わる点を
と交わる点を![]() とする.
とする.
![]() から
から![]() に
に![]() とは異なる接線をひき,
その延長が再び
とは異なる接線をひき,
その延長が再び![]() と交わる点を
と交わる点を![]() とする.
とする.
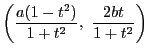 と
媒介変数表示できることを示せ.
と
媒介変数表示できることを示せ.
また,
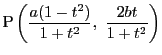 ,
,
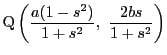 とするとき,直線
とするとき,直線![]() が
が![]() と接するための
と接するための![]() と
と![]() に関する条件を求めよ.
に関する条件を求めよ.
拓生 これもできそうです.
解答
(1)
楕円![]() 上の点の座標は
上の点の座標は
![]() と表されるので, これを
と表されるので, これを![]() で表すと,
で表すと,
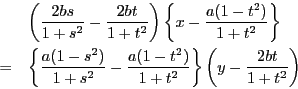
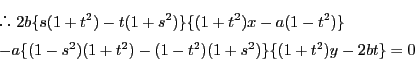
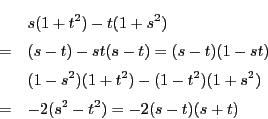
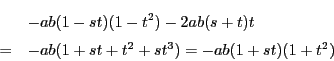
(2)
ここでも
![]() とする.
このとき
とする.
このとき![]() は
は![]() の二次方程式で,
の二次方程式で,
![]() がその2解となるので, 解と係数の関係より,
がその2解となるので, 解と係数の関係より,
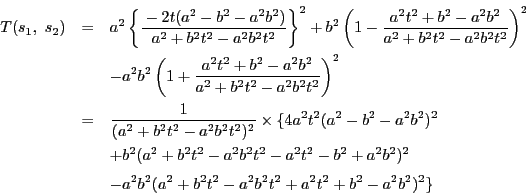
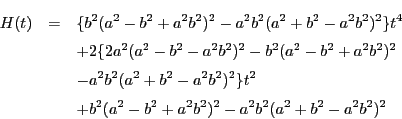
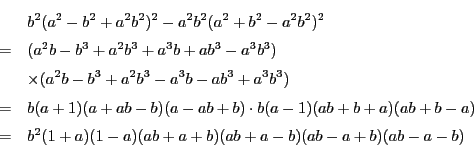
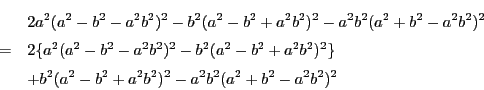
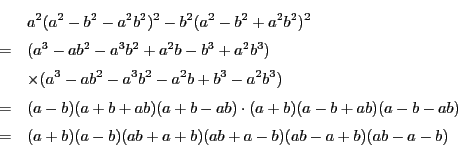
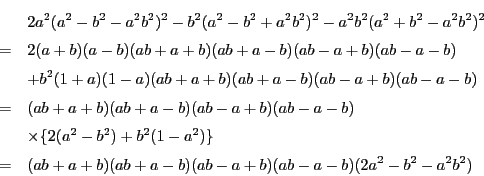
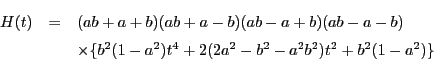
(3)
![]() のとき,
のとき,![]() を
を![]() の二次式と見たときの軸は
の二次式と見たときの軸は
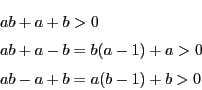
南海
ここで一つ注意したい.
(3)で求めた![]() の定数を除いた部分は
(2)で求めた
の定数を除いた部分は
(2)で求めた![]() において
において
拓生
本当だ.これは接線の定義から
![]() が
が
![]() での接線になるのですね.
ということはこの場合
での接線になるのですね.
ということはこの場合![]() は
は![]() と
と![]() の共通接線を与える
の共通接線を与える![]() の条件ということになります.
の条件ということになります.
南海 その意味は後に考えよう.
証明
![]() より,
より,
 南海
さて,
南海
さて,![]() のときは,
のときは,![]() と
と![]() を考える.
これから
を考える.
これから![]() を消去する.
すると
を消去する.
すると![]() から2回目の操作で定まる点の座標を与える2次方程式が得られるはずだ.
から2回目の操作で定まる点の座標を与える2次方程式が得られるはずだ.
この2次方程式が重解をもてば,つまり図で![]() となれば,確かに4回で閉じる.
それが
となれば,確かに4回で閉じる.
それが![]() を頂点とし,
を頂点とし,![]() に外接し,
に外接し,![]() に内接する四角形が存在するための
に内接する四角形が存在するための![]() に関する必要十分条件になるはずだ.
に関する必要十分条件になるはずだ.
拓生
やってみます.
![]() から
から![]() を消去し,
を消去し,
![]() の条件の下で
の条件の下で![]() の関係式を求める.
の関係式を求める.
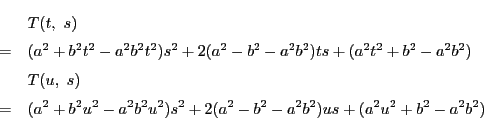
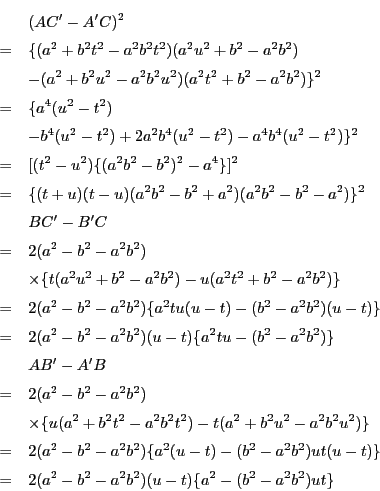
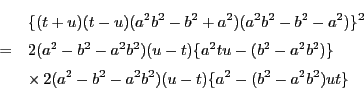
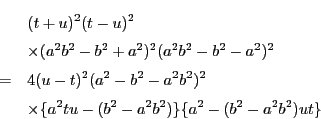
![\begin{eqnarray*}
&& (t+u)^2(a^2-b^2+a^2b^2)^2(a^2+b^2-a^2b^2)^2 \\
&=&4(a^...
...(b^2-a^2b^2)t^2u^2+\{a^4+(b^2-a^2b^2)^2\}ut
-a^2(b^2-a^2b^2)]
\end{eqnarray*}](images/img237.gif)
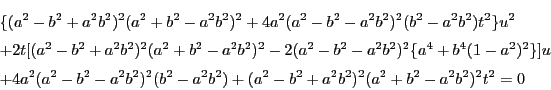
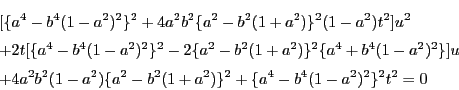
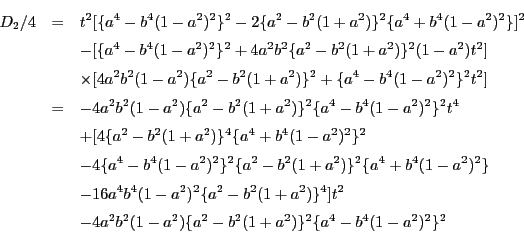
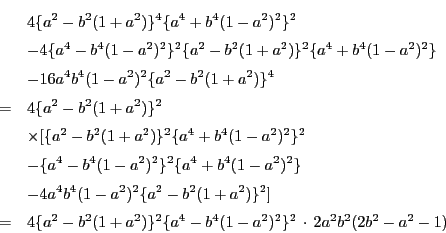
![\begin{eqnarray*}
D_2/4
&=&-4\{a^2-b^2(1+a^2)\}^2\{a^4-b^4(1-a^2)^2\}^2 \\
...
...^2\}^2a^2b^2\\
&&\times[(a^2-1)t^4+2(2b^2-a^2-1)t^2+(a^2-1)]
\end{eqnarray*}](images/img244.gif)
拓生
![]() が
が![]() が満たすべき条件式です.
そこで,
が満たすべき条件式です.
そこで,
![\begin{eqnarray*}
H(t)&=&4\{a^2-b^2(1+a^2)\}^2\{a^4-b^4(1-a^2)^2\}^2a^2b^2\\
&&\times[(a^2-1)t^4+2(2b^2-a^2-1)t^2+(a^2-1)]
\end{eqnarray*}](images/img246.gif)
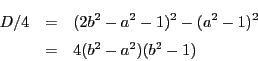
![]() のとき,
のとき,![]() を
を![]() の二次式と見たときの軸は
の二次式と見たときの軸は
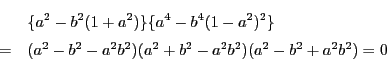
南海 ここで得られた条件は,東大の問題の結果と同じだ.
拓生
![]() のときの
のときの![]() と
と![]() のときの
のときの![]() の式は違いますが,
その判別式の正負は同じです.
の式は違いますが,
その判別式の正負は同じです.
南海 そうだ.その意味は何かあるのだろうが宿題にしておこう.