耕一 楕円でやってみます.
焦点をF(c,0),F'(-c,0)とし,
![]() とします.
楕円の定義から
とします.
楕円の定義から
南海 パッポスの定義との関連を見るために
ただしこれは,
![]() が正となるところにPがあるときだ.
が正となるところにPがあるときだ.
耕一
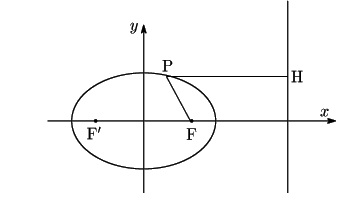 南海
(2)と辺々引いて2で割ると
南海
(2)と辺々引いて2で割ると
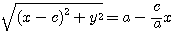
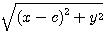 = PF
= PF
このとき
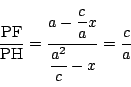
この式変形を逆にたどることで, パッポスによる定義で定まる曲線がアポロニウスの定義をみたすことが示され, 二つの定義が同等であることがわかる.
双曲線の場合,放物線の場合にもまったく同様な関係が成り立つ. これは演習問題としておこう.
南海
まとめると次のようになるはずだ.これを確認することを演習でやってほしい.
