楕円や双曲線,放物線が二次曲線といわれるのはなぜか.
耕一
曲線を定義する方程式が
南海 しかし二次式ということになると他にいくらもある.
耕一
『数学対話』−「パスカルの定理」のなかにあるように,![]() と
と![]() の二次式の一般形は
の二次式の一般形は
これをみたす点![]() の全体が,方程式(3)で定まる図形ということになります.
の全体が,方程式(3)で定まる図形ということになります.
『数学対話』−「シュタイナー楕円」のなかに,![]() のときには,
この方程式で定まる図形を平行移動したり,一次変換で移動すると,
標準形で表された二次曲線の方程式が得られることが書かれています.
のときには,
この方程式で定まる図形を平行移動したり,一次変換で移動すると,
標準形で表された二次曲線の方程式が得られることが書かれています.
南海 よく勉強している. その内容を整理して再掲しよう.
最も一般的な考え方は
『数学対話』−「線型代数の考え方」−「内積と直交変換」−「内積の対角型行列表示」にある.
この対話の最後の演習問題にもあるのだが,ここでは,
数学![]() の範囲内で,この二次曲線を移動して標準形で表されるようにする手順を考えよう.
の範囲内で,この二次曲線を移動して標準形で表されるようにする手順を考えよう.
方程式(3)で定まる図形を回転と平行移動して標準形にするのである.
平行移動は先にしても後からしてもいいのだが,
ここでは後からすることにし,まず![]() という項を消すために回転しよう.
という項を消すために回転しよう.
![]() を回転行列
を回転行列
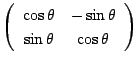 とし,
二次曲線
とし,
二次曲線
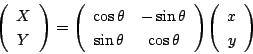
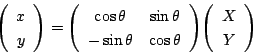
耕一
![]() の部分で考えればよいです.
の部分で考えればよいです.

\begin{eqnarray*} A&=&\dfrac{a+b}{2}+\dfrac{a-b}{2}\cos2\theta-h\sin2\theta\\ B&=&\dfrac{a+b}{2}-\dfrac{a-b}{2}\cos2\theta+h\sin2\theta\\ H&=&-\dfrac{b-a}{2}\sin2\theta+h\cos2\theta\\ \end{eqnarray*}
です.
南海
![]() が成り立つはずだ.
が成り立つはずだ.
耕一
\begin{eqnarray*} A+B&=&a+b\\ AB-H^2&=&\left(\dfrac{a+b}{2} \right)^2-\left(\dfrac{a-b}{2}\cos2\theta-h\sin2\theta \right)^2\\ &&\quad \quad -\left(-\dfrac{b-a}{2}\sin2\theta+h\cos2\theta\right)^2\\ &=&\dfrac{(a+b)^2}{4}-\dfrac{(a-b)^2}{4}-h^2=ab-h^2 \end{eqnarray*}
です.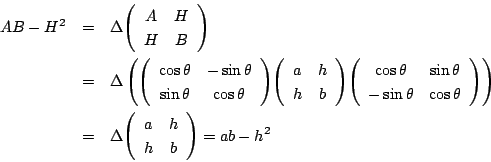
そこで,![]() ならば
ならば
![]() にとり,
にとり,
![]() ならば
ならば
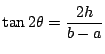 となる
となる![]() をとれば
をとれば
![]() になります.
になります.
南海
回転,一般的には一次変換で![]() の部分は
の部分は![]() と
と![]() の一次式になることはまちがいない.
回転角を適当にとることで(3)が
の一次式になることはまちがいない.
回転角を適当にとることで(3)が
耕一
一次の項は平行移動で消せる.
また,![]() にしたときは
にしたときは![]() なので,
なので,![]() か
か![]() に応じて楕円か双曲線になります.
に応じて楕円か双曲線になります.
南海 とはかぎらない.(4)が因数分解されるときがある.
耕一 そうか. 因数分解できるということは,図形が2直線になるということですね.
南海 そうだ.回転して2直線になるということは,もともと2直線だから, このときは(3)がすでに因数分解される.
耕一
では![]() のときは,どのようになるのですか.
のときは,どのようになるのですか.
南海
![]() ならば
ならば
![]() にとり,
にとり,
![]() ならば
ならば
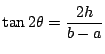 となる
となる![]() をとれば,
をとれば,
![]() とできることは同様だ.
とできることは同様だ.
さらに![]() の場合は
の場合は![]() となる.
となる.
したがって![]() にしたとき
にしたとき![]() となるのだ.
となるのだ.
耕一
![]() か
か![]() ならそれぞれ
ならそれぞれ![]() 軸または
軸または![]() 軸に平行な放物線です.
軸に平行な放物線です.
![]() なら,必然的に
なら,必然的に![]() で,このときは
で,このときは![]() も成り立ち(3)が二次式でなくなります.
も成り立ち(3)が二次式でなくなります.
南海
さらに,
この場合も結局は(3)が
以上から(3)で定まる図形は
楕円,双曲線,放物線のいずれかになる.
円
2直線,1直線
1点,空集合
ところで,方程式(3)は3次対称行列を用いると
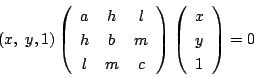
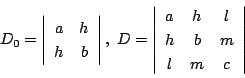
このとき