というものだ.四面体にも外心と内心がある. ここにはどのような関係が成り立つのだろうか. これに関する定理を「空間でのチャップル型定理」と言おう. これについて次の命題が成立する. これは『幾何学大辞典』の第4巻にあり, 辞典の著者である岩田至康さんによる命題である.の内心をIとし, 内接円の半径を
とする. また,外心をOとし, 外接円の半径を
とすると,
である.
頂点Aと内心Iを交換した四面体IBCDの外心を
![]() とし,他も同様に定める.このとき四面体
とし,他も同様に定める.このとき四面体
![]() の外心はOに一致し,外接球の半径を
の外心はOに一致し,外接球の半径を![]() とおくと
とおくと
![]() である.
■
である.
■
![]() は
四面体ABCDの各頂点を通る球の方程式であり,
は
四面体ABCDの各頂点を通る球の方程式であり,
![]() は,3点B,C,Dを通る平面の方程式である.
よって,
は,3点B,C,Dを通る平面の方程式である.
よって,
![\begin{eqnarray*}
&&[
\overrightarrow{u}-\overrightarrow{b},\
\overrightarro...
...
\overrightarrow{b},\ \overrightarrow{c},\ \overrightarrow{d}]
\end{eqnarray*}](images/img246.gif)
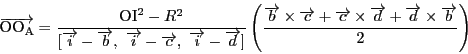
![$\dfrac{1}{6}[
\overrightarrow{i}-\overrightarrow{b},\
\overrightarrow{i}-\overrightarrow{c},\
\overrightarrow{i}-\overrightarrow{d}
]$](images/img248.gif) が,四面体IBCDの体積である.
これは,内接円の半径を高さとし,
が,四面体IBCDの体積である.
これは,内接円の半径を高さとし,
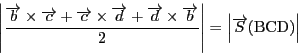
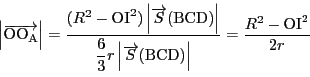
耕一 これは平面の場合のチャップルの定理の拡張なのですか. 平面の場合のチャップルの定理は,円周角の定理まで用いたはずですが, 四面体の場合は線型代数だけでできました.
南海
平面の場合は![]() となる.
その証明に円周角の定理がいる.
そこに平面の場合の難しさがあった.
これについては2009年の京大の入試問題乙2番6
を見てほしい.
となる.
その証明に円周角の定理がいる.
そこに平面の場合の難しさがあった.
これについては2009年の京大の入試問題乙2番6
を見てほしい.
四面体のこの命題は線型代数の範囲の命題であり,
ここまでなら![]() 次元の場合にも拡張できるだろう.
それは今はおくが,試みてほしい.
次元の場合にも拡張できるだろう.
それは今はおくが,試みてほしい.
等面四面体では外心と内心が一致するので,命題1は,
証明
![]() を
$ a^2+b^2+c^2=1 $
を満たす正の定数とし,
を
$ a^2+b^2+c^2=1 $
を満たす正の定数とし,
![]() 空間上の四面体ABCDを
空間上の四面体ABCDを
![]() ,
,
![]() ,
,
![]() ,
,
![]() で定める.
で定める.
このとき,四面体 ABCD の各面は, \[ \sqrt{a^2+b^2},\ \sqrt{b^2+c^2},\ \sqrt{c^2+a^2} \] を3辺の長さとする合同な三角形である.
球
![]() は,四面体の中心である内心とABC平面
は,四面体の中心である内心とABC平面
次に,3点A,B,Cと中心
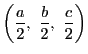 を通る球を
を通る球を
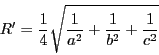
コーシー・シュワルツの不等式から
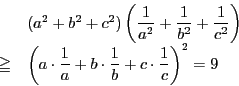
これは平面の場合のチャップル型定理と同様のものである.
これがどのように一般化されるかは,未解決である.