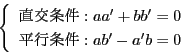耕一
平行ということは方向が同じで大きさは違ってもよいということなので,
0でない実数 ![]() で
で
![]() と
と
![]() が平行,
つまり
が平行,
つまり
![]() なる
なる ![]() があるとします.このとき
があるとします.このとき
逆に
![]() とします.
とします.
![]() なら
なら![]() なので
なので![]() となり
となり
![]() と
と
![]() は平行,
は平行,
![]() のときも同様.
のときも同様.
![]() とする.
このとき
とする.
このとき
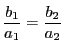 となる.この比の値を
となる.この比の値を ![]() とすると,
とすると,
これは二つのベクトル
![]() と
と
![]() から作られる行列
から作られる行列
南海
逆に平行でないということは
![]() であり,
このとき行列
であり,
このとき行列![]() は逆行列
は逆行列
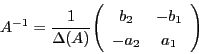
耕一
任意のベクトル
![]() に対して
に対して
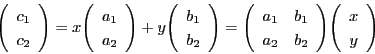
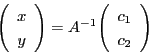
つまり二つのベクトル
![]() とベクトル
とベクトル
![]() が一次独立ならば,
これを用いて任意のベクトル
が一次独立ならば,
これを用いて任意のベクトル
![]() を表すことができる.
を表すことができる.
南海
ということなのだ.
だからやはり平面ベクトルの理解も一次変換と行列までの内容を必要とする.
このことはさらに3次元,![]() 次元ベクトルについても言える.
次元ベクトルについても言える.
なお,行列
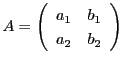 に対して,
数
に対して,
数![]() のことを行列
のことを行列![]() の行列式といい
の行列式といい
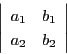
耕一
直線 ![]() 上の点を
上の点を
![]() とおく.この
とおく.この ![]() と
と ![]() が
満たす式を求めればよいのですね.
が
満たす式を求めればよいのですね.
![]() が直線
が直線 ![]() 上にあるということは二つのベクトル
上にあるということは二つのベクトル
南海
そうだ.これは昔どおり傾きを求めてから導く直線の式と同じだろう.
![]() のとき (1)はまた
のとき (1)はまた
これと本質的に同じだが,ほんの少し違う形で導こう.
耕一
(3)式を成分で書くと
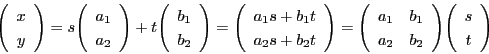
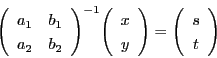
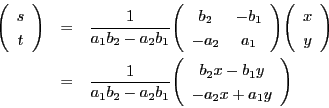
南海
式が同じになるのは当然なのだが,なかなかおもしろい.
行列を習っていない人は,![]() と
と![]() を未知数として連立一次方程式を解いたと考えればよい.
を未知数として連立一次方程式を解いたと考えればよい.
![]() でない二つのベクトル
でない二つのベクトル
![]() と
と
![]() が直交している条件は,二つのベクトルのなす角が
が直交している条件は,二つのベクトルのなす角が
![]() ,
つまり内積が0ということなので,
,
つまり内積が0ということなので,
耕一
これは教科書にも載っています.直線上の任意の点
![]() をとる.
をとる.
二つのベクトル
![]() と
と
![]() が直交するので内積が0.
が直交するので内積が0.
![]() なので
なので
南海
その通り.
逆に直線の方程式 ![]() からはじめると,
この直線とベクトル
からはじめると,
この直線とベクトル ![]() は平面上でたがいに直交している.
なぜか.
は平面上でたがいに直交している.
なぜか.
耕一
この方程式を満たす任意の2点
![]() をとる.
をとる.
これは,方程式![]() をみたす点の集合が,
点
をみたす点の集合が,
点
![]() を通りベクトル
を通りベクトル![]() と直交する直線になることを示している.
と直交する直線になることを示している.
南海
二つの直線
![]() に対して二つの法線ベクトル
に対して二つの法線ベクトル
![]() ができるが,
もとの二直線が直交または平行であるのに応じて,
それぞれの法線ベクトルも直交または平行であるから,上の二直線の
ができるが,
もとの二直線が直交または平行であるのに応じて,
それぞれの法線ベクトルも直交または平行であるから,上の二直線の