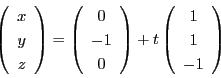次: 外積と図形
上: 座標空間での直線と平面
前: 平面上の直線
次: 外積と図形
上: 座標空間での直線と平面
前: 平面上の直線
南海
さて以上の議論を空間内の,つまりは3次元の場合に拡張せよ.これが問題だ.
空間の場合には,平面における直線と対応するのは,空間における平面である.
平面の定め方も二通りある.
耕一
第一は,同一直線上にない三点で平面が定まる.
第二は,ある点をとおり,与えられたベクトルに垂直な直線の全体が一つの平面となる.
ということです.それぞれどのような式になるかを考えます.
耕一
空間に同一直線上にない3点,
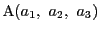 ,
,
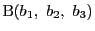 ,
,
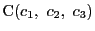 がある.
点
がある.
点
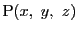 がこの三点で定まる平面上にあるための必要十分条件を
がこの三点で定まる平面上にあるための必要十分条件を
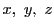 の関係式で書けば,それが求める平面の方程式です.
の関係式で書けば,それが求める平面の方程式です.
これはベクトル
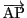 が
ベクトル
が
ベクトル
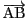 と
ベクトル
と
ベクトル
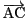 でかき表せることと同値です.
これを
でかき表せることと同値です.
これを
とおき,始点を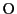 にそろえると
にそろえると
となります.
このことから,
点
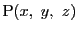 が,
3点
が,
3点
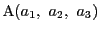 ,
,
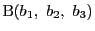 ,
,
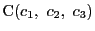 で定まる平面上にあるための必要十分条件を次のようにいってもよいことがわかります.つまり
で定まる平面上にあるための必要十分条件を次のようにいってもよいことがわかります.つまり
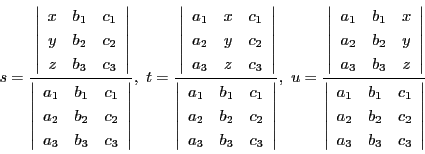
とおくとき,点 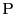 がこの平面上にあるための必要十分条件は
がこの平面上にあるための必要十分条件は
である.
この条件を成分で書くと
これから
によって, 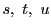 を
を 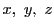 で表し,
で表し, 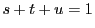 に代入すれば,
平面の方程式が得られる.
に代入すれば,
平面の方程式が得られる.
南海
高校範囲では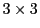 行列の逆行列は求まらないが,
空間における平面の方程式が
行列の逆行列は求まらないが,
空間における平面の方程式が
という形の1次の等式になることはわかった.
次の3点をとおる平面の方程式をいろんな方法で求めてみよう.
例 1.1
3点で定まる平面の方程式;
-
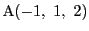 ,
,
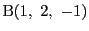 ,
,
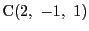
-
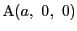 ,
,
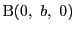 ,
,
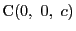
-
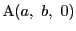 ,
,
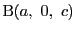 ,
,
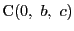
南海
もっとも,3次の行列式を用いれば平面の方程式を一般的な形に書くことが出来る.
点
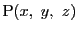 が3点
が3点
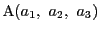 ,
,
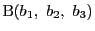 ,
,
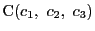 で定まる平面上にあることと,
ベクトル
で定まる平面上にあることと,
ベクトル
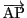 が
ベクトル
が
ベクトル
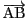 と
ベクトル
と
ベクトル
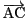 でかき表せること,
言いかえれば,三つのベクトル
でかき表せること,
言いかえれば,三つのベクトル
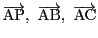 が一次従属ということとが同値だ.
したがってその行列式は0,つまり
が一次従属ということとが同値だ.
したがってその行列式は0,つまり
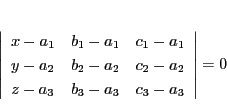 |
(4) |
である.これが3点を通る平面の方程式だ.
この一般論は『線型代数の考え方』を見てほしい.
耕一
これが,
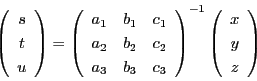 |
(5) |
で定まる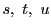 を
を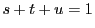 に代入した式と一致するのですか.
に代入した式と一致するのですか.
南海
次のように考えればよい.行列式展開の計算から
(4)は
と変形される.ただし展開と考えなくても,この等式は,
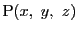 にA,B,Cの座標値を代入して成立するので,
この3点を通る平面の方程式であることがわかる.
にA,B,Cの座標値を代入して成立するので,
この3点を通る平面の方程式であることがわかる.
次に5を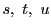 に関する連立1次方程式と見れば
に関する連立1次方程式と見れば
となる.ここは『線型代数の考え方』「クラメルの公式」を見てほしい.
それからさらに列を入れ替えると,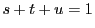 を満たすこととの同値性が分かる.
を満たすこととの同値性が分かる.
もっとも(4)も(5)も3つのベクトル
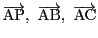 が1次従属になる条件の同値な変形なのだから,
互いに同値な条件であること,したがって方程式も一致する.
が1次従属になる条件の同値な変形なのだから,
互いに同値な条件であること,したがって方程式も一致する.
南海
平面はもう一つの定義がある.
それは線型空間では直交補空間といわれるのであるが,
定点を通り,
点と定点を結ぶ直線があたえられた方向と直交するような点の集合としての平面である.
この立場から定点
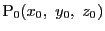 をとおり,
ベクトル
をとおり,
ベクトル
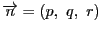 に直交する平面
に直交する平面 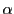 の方程式を求めよ.
の方程式を求めよ.
耕一
平面上の任意の点
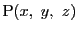 をとる.
二つのベクトル
をとる.
二つのベクトル
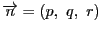 と
と
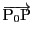 が直交するので内積が0.
が直交するので内積が0.
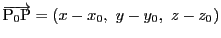 なので
なので
です.
このベクトル
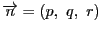 のことを
平面
のことを
平面 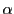 の法線ベクトルという.
の法線ベクトルという.
南海
逆に一次式 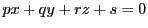 を満たす点
を満たす点 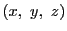 はどんな図形になるかも同様にわかる.
はどんな図形になるかも同様にわかる.
耕一
この式を満たす任意の2点
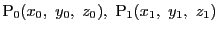 をとる.
をとる.
より
つまりベクトル 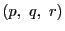 と直線
と直線
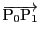 が直交している.
したがって求める図形は点
が直交している.
したがって求める図形は点
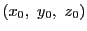 をとおりベクトル
をとおりベクトル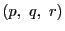 と直交する直線の集合,
平面になる.
と直交する直線の集合,
平面になる.
空間の点と平面の距離の公式も,点と直線の場合と同様に求められる.
耕一
点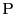 から平面
から平面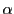 への垂線の足を
への垂線の足を
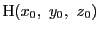 とする.
ベクトル
とする.
ベクトル
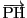 は平面
は平面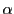 と直交するので,
と直交するので,
これから
つまり
点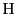 は平面
は平面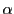 上にあるので
上にあるので
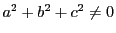 なので
なので
である.
一方
であるから
となる.よって
である.
耕一
では空間内の直線はどのように表されるのでしょうか.
南海
空間における直線は二つの平行でない平面の交わりによって定まる.だから
方程式としては,二つの一次式の連立で表される.
例えば
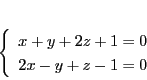 |
(6) |
なども二平面の交わりとして何らかの直線を表す.しかしそれがどのような直線かは
このままではわからない.
耕一
点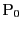 をとおりベクトル
をとおりベクトル
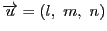 に平行な直線は
動点を
に平行な直線は
動点を 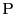 とすれば
とすれば
と表されます.
南海
それを座標で書くとどうなるか.
耕一
です.そうすると
ですから 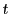 を消去すると
を消去すると
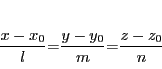 |
(7) |
ですか.確かに等号が二つある.
南海
この考え方でいくと(6)はどんな直線なのか.
耕一
二式を加えると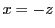 .これから
.これから 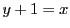 .これを(7)の形に書くと
.これを(7)の形に書くと
するとこれは定点 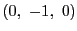 をとおりベクトル
をとおりベクトル
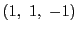 に平行な直線なんだ.ベクトルを用いて書けば
に平行な直線なんだ.ベクトルを用いて書けば
ということです.


 次: 外積と図形
上: 座標空間での直線と平面
前: 平面上の直線
Aozora
2018-08-31
次: 外積と図形
上: 座標空間での直線と平面
前: 平面上の直線
Aozora
2018-08-31
![]() が
ベクトル
が
ベクトル
![]() と
ベクトル
と
ベクトル
![]() でかき表せることと同値です.
これを
でかき表せることと同値です.
これを
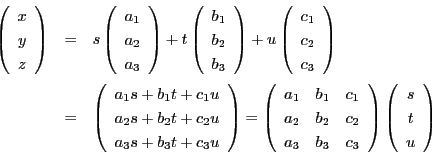
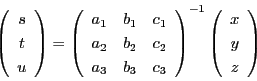
![]() 行列の逆行列は求まらないが,
空間における平面の方程式が
行列の逆行列は求まらないが,
空間における平面の方程式が
![]() が3点
が3点
![]() ,
,
![]() ,
,
![]() で定まる平面上にあることと,
ベクトル
で定まる平面上にあることと,
ベクトル
![]() が
ベクトル
が
ベクトル
![]() と
ベクトル
と
ベクトル
![]() でかき表せること,
言いかえれば,三つのベクトル
でかき表せること,
言いかえれば,三つのベクトル
![]() が一次従属ということとが同値だ.
したがってその行列式は0,つまり
が一次従属ということとが同値だ.
したがってその行列式は0,つまり
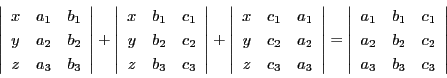
![]() に関する連立1次方程式と見れば
に関する連立1次方程式と見れば
![]() が1次従属になる条件の同値な変形なのだから,
互いに同値な条件であること,したがって方程式も一致する.
が1次従属になる条件の同値な変形なのだから,
互いに同値な条件であること,したがって方程式も一致する.
![]() をとおり,
ベクトル
をとおり,
ベクトル
![]() に直交する平面
に直交する平面 ![]() の方程式を求めよ.
の方程式を求めよ.
![]() をとる.
二つのベクトル
をとる.
二つのベクトル
![]() と
と
![]() が直交するので内積が0.
が直交するので内積が0.
![]() なので
なので
![]() を満たす点
を満たす点 ![]() はどんな図形になるかも同様にわかる.
はどんな図形になるかも同様にわかる.
![]() をとる.
をとる.
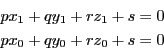
![]() から平面
から平面![]() への垂線の足を
への垂線の足を
![]() とする.
ベクトル
とする.
ベクトル
![]() は平面
は平面![]() と直交するので,
と直交するので,
![]() をとおりベクトル
をとおりベクトル
![]() に平行な直線は
動点を
に平行な直線は
動点を ![]() とすれば
とすれば
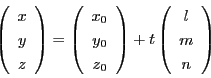
![]() .これから
.これから ![]() .これを(7)の形に書くと
.これを(7)の形に書くと