

 次: 符号のある面積
上: 外積と図形
前: 外積と図形
次: 符号のある面積
上: 外積と図形
前: 外積と図形
南海
二つのベクトル
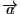 と
と
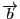 がある.
ベクトル
がある.
ベクトル
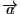 からベクトル
からベクトル
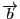 へ右ネジを回転させたとき,
ネジの進む方向の単位ベクトルを
へ右ネジを回転させたとき,
ネジの進む方向の単位ベクトルを
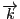 とおく.
また
とおく.
また
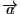 と
と
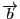 のなす角を
のなす角を
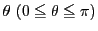 とおく.
とおく.
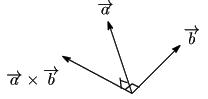 このときベクトル
このときベクトル
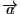 と
と
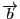 の外積を次式で定める.
の外積を次式で定める.
耕一
内積の時と同様に,
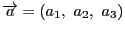 と
と
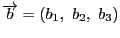 に対して
に対して
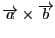 を成分で表してみます.
を成分で表してみます.
大きさは
です.
これは,二つのベクトル
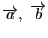 でできる平行四辺形の面積です.
しかしこの大きさをもつベクトルで,方向が右ネジの進む方向になるものをどのように作ればよいのか.
でできる平行四辺形の面積です.
しかしこの大きさをもつベクトルで,方向が右ネジの進む方向になるものをどのように作ればよいのか.
南海
結論的にいうと
とすればよい.
耕一
確かに大きさは
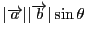 になります.
また
になります.
また
ですから
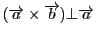 ,同様に
,同様に
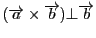 も成り立ちます.
も成り立ちます.
でも,右ネジの進む方向というのはどのように確認すればよいのかわかりません.
南海
後は方向の問題だけなので,二つのベクトルをその間の角をかえないように回転し
それらのベクトルが
となるようにしてみる.
これはかならずできる.このとき
となり,
確かに
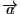 から
から
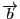 へ右ネジを回したときの進む方向になっている.
へ右ネジを回したときの進む方向になっている.
したがって外積は次のような計算法則を満たす.
耕一
外積は二つのベクトルに直交するベクトルを作るのに便利です.
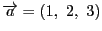 と
と
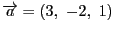 に直交する方向が知りたければ
連立方程式
に直交する方向が知りたければ
連立方程式
を解かねばなりません.この連立方程式はすぐ解けます.が,一般には外積を使う方が簡単です.
が得られます.
南海
次の補題は後で図形問題に応用するため必要だ.
証明
とする.
-
-
とし,
とする.
ここで,左辺の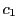 のかかるベクトル
のかかるベクトル
一方,右辺の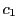 のかかるベクトルは
のかかるベクトルは
で等しい.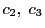 についても同様に成り立つ.したがって(2)が成立する.
についても同様に成り立つ.したがって(2)が成立する.
- (2)と同様に
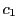 にかかる係数について
にかかる係数について
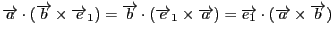 を示せばよい.
を示せばよい.
これが
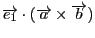 に
一致するのは明らか.よって(3)が示された.□
に
一致するのは明らか.よって(3)が示された.□
南海
(3)の等式の値は,3次行列式を用いると
に一致する.
耕一
確認します.
これは(3)の別証明になっています.つまり同様にして
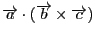 も
も
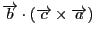 も
も
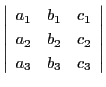 に一致することが示されるからです.
に一致することが示されるからです.
したがってこれはベクトル
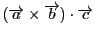 から
作られる行列式そのものである.
から
作られる行列式そのものである.
南海
とおき,スカラー3重積という.
が成り立つ.


 次: 符号のある面積
上: 外積と図形
前: 外積と図形
Aozora
2018-08-31
次: 符号のある面積
上: 外積と図形
前: 外積と図形
Aozora
2018-08-31
 このときベクトル
このときベクトル
 このときベクトル
このときベクトル
![]() と
と
![]() の外積を次式で定める.
の外積を次式で定める.
![]() と
と
![]() に対して
に対して
![]() を成分で表してみます.
を成分で表してみます.
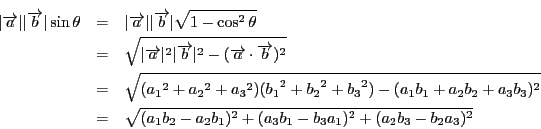
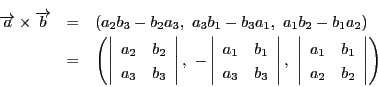
![]() になります.
また
になります.
また
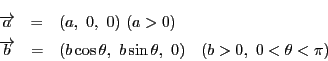
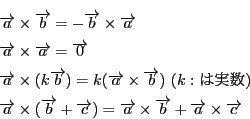
![]() と
と
![]() に直交する方向が知りたければ
連立方程式
に直交する方向が知りたければ
連立方程式
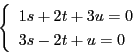
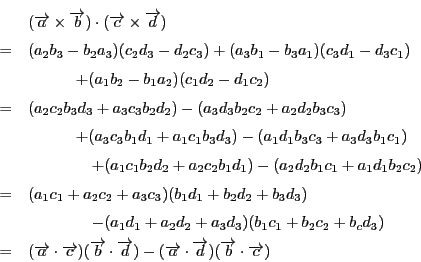
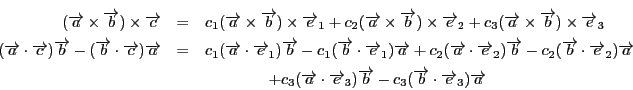
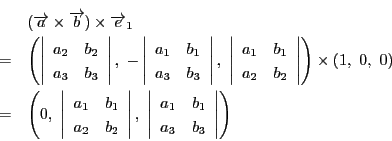
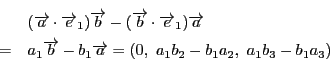
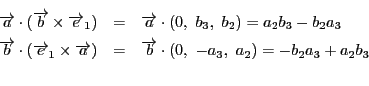
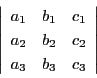
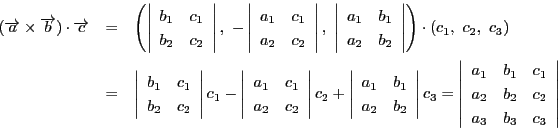
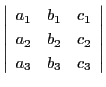 に一致することが示されるからです.
に一致することが示されるからです.
![]() から
作られる行列式そのものである.
から
作られる行列式そのものである.