次: 四面体の諸命題 上: 外積と図形 前: 符号のある面積

四面体とベクトル

南海　 三角形の面積に関する関係式(8)が四面体の体積についても成り立つ． そのためにまず符号付きの四面体の体積を定義しよう．

符号付き体積

原点Oと3点A，B，Cが同一平面上にないとする． このとき四面体OABCの体積$V$をA，B，Cの座標成分を用いて

$$V=\dfrac{1}{6} \left\vert \begin{array}{ccc} a_1&b_1&c_1\\ a_2&b_2&c_2\\ a_3&b_3&c_3 \end{array} \right\vert$$

で定める．

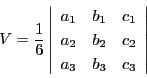
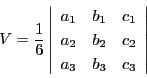
耕一　 これは実際に四面体の体積になっているか確認します．

$\bigtriangleup \mathrm{OBC}$の面積は

$$\begin{eqnarray*} &&\dfrac{1}{2}\sqrt{\vert\overrightarrow{\mathrm{OB}}\vert^2\... ...rray}{cc} b_1&c_1\\ b_2&c_2 \end{array} \right\vert^2} \end{eqnarray*}$$

となります． 一方， $\bigtriangleup \mathrm{OBC}$のある平面の方程式は， 平面上の点 $\mathrm{P}(x,\ y,\ z)$が$\mathrm{OB}$，$\mathrm{OC}$に一次従属するので，

$$\left\vert \begin{array}{ccc} x&b_1&c_1\\ y&b_2&c_2\... ...}{cc} b_1&c_1\\ b_2&c_2 \end{array} \right\vert z=0$$

です．この結果，点$\mathrm{A}$とこの平面との距離は

$$\dfrac{\left\vert\left\vert \begin{array}{ccc} a_1&b_1&... ...y}{cc} b_1&c_1\\ b_2&c_2 \end{array} \right\vert^2}}$$

です．ですから，これまでの方法での体積は次のようになります．

$$\begin{eqnarray*} V&=&\dfrac{1}{3}\times \dfrac{1}{2}\sqrt{ \left\vert \beg... ...&b_2&c_2\\ a_3&b_3&c_3 \end{array} \right\vert\right\vert \end{eqnarray*}$$

これは，上記の定義に絶対値がついたものです．

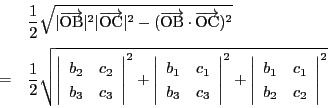
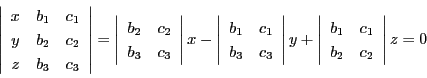
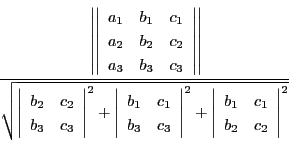
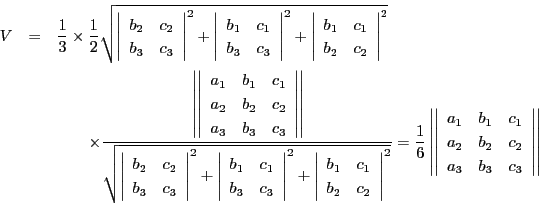
この符号はどのようになるのですか．

南海　 $a_1=b_2=c_3=1$，他の成分は0としたとき正になる． いいかえるとA，B，CがOを基準に右手の法則，つまり 親指がOA，人差し指がOB，中指がOCとなる順に並んでいるとき この体積は正になる．

この値は先ほど定義したスカラー3重積である．つまり，

$$V=\dfrac{1}{6}[\overrightarrow{a},\ \overrightarrow{b},\ \overrightarrow{c}]$$

である．

次に，四面体ABCDで頂点の位置ベクトルを $\overrightarrow{a},\ \overrightarrow{b},\ \overrightarrow{c},\ \overrightarrow{d}$とする． このとき体積 $V(\mathrm{ABCD})$を

$$V(\mathrm{ABCD})= \dfrac{1}{6}[\overrightarrow{a}-\overrig... ...\overrightarrow{d},\ \overrightarrow{c}-\overrightarrow{d}]$$

で定める．位置ベクトルの基準点をOとすると

$$\begin{eqnarray*} 6V(\mathrm{ABCD})&=& [\overrightarrow{a},\ \overrightarrow{b... ...rm{ABCO})+6V(\mathrm{ABOD})+6V(\mathrm{AOCD})+6V(\mathrm{OBCD}) \end{eqnarray*}$$

と，D，C，B，Aを順にOに入れ替えた体積の和となる． これが面積のときの等式(8)に対応する体積の等式である．

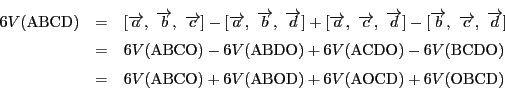
ここで点と位置ベクトルを同一視するなら次のようなことも導かれる．

点 $\overrightarrow{d}$が $\overrightarrow{a},\ \overrightarrow{b},\ \overrightarrow{c}$で定まる平面上の点であることと， 面積が0であることが同値なので， 点 $\overrightarrow{d}$を動点 $\overrightarrow{u}$にかえることにより， $\overrightarrow{a},\ \overrightarrow{b},\ \overrightarrow{c}$で定まる平面の方程式が

$$\begin{eqnarray*} &&[ \overrightarrow{u}-\overrightarrow{a},\ \overrightarro... ...verrightarrow{a},\ \overrightarrow{b},\ \overrightarrow{c}] =0 \end{eqnarray*}$$

と表される．

南海　 平面の三角形の面積は，正負の符号がついた． 空間の三角形ABCに対しては，次のように面積ベクトルを定める．

面積ベクトル

$$\begin{eqnarray*} \overrightarrow{S}(\mathrm{ABC}) &=&\dfrac{1}{2}(\overrighta... ...arrow{c}+ \overrightarrow{c}\times\overrightarrow{a} \right) \end{eqnarray*}$$

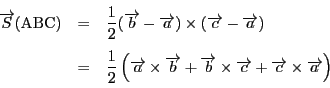
耕一　 $\overrightarrow{S}(\mathrm{ABC})$の 大きさは $\bigtriangleup \mathrm{ABC}$の面積の大きさと同じで， 方向は， $\bigtriangleup \mathrm{ABC}$の面積が正のとき， つまりA，B，Cが左回りのとき，手前にABC平面と直交する方向になります．