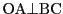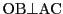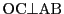
次: 四面体の重心と平行六面体への埋め込み 上: 特別な四面体 前: 特別な四面体

ある入試問題

拓生　 2003年の京大入学試験で次の問題が出ました．

例 0.1.1   四面体OABCは次の2つの条件

1. $\mathrm{OA}\bot\mathrm{BC}$， $\mathrm{OB}\bot\mathrm{AC}$， $\mathrm{OC}\bot\mathrm{AB}$
2. 4つの面の面積がすべて等しい．

をみたしている．このとき，この四面体は正四面体であることを示せ．

この問題は面積をベクトルで表せればすぐにできます．

南海　 そう．文系の方はベクトルで与えられ，理系の方は線分で与えられていた．

拓生　 いずれにしてもベクトルで解くのが一番簡単なようです．

解答

$\overrightarrow{\mathrm{OA}} =\overrightarrow{\mathstrut a}$, $\overrightarrow{\mathrm{OB}}=\overrightarrow{\mathstrut b}$, $\overrightarrow{\mathrm{OC}} =\overrightarrow{\mathstrut c}$ とおくと, 条件(i)より

$$\overrightarrow{\mathstrut a}\cdot\left(\overrightarrow{\ma... ...ghtarrow{\mathstrut b}-\overrightarrow{\mathstrut a}\right)=0$$

$$∴\quad \overrightarrow{\mathstrut a}\cdot\overrightarrow{\... ...rut c}\cdot\overrightarrow{\mathstrut a} \quad\cdots\maru{1}$$

また, 条件(ii)より

$$\triangle{\rm OAB}=\triangle{\rm OBC}=\triangle{\rm OCA}$$

なので

$$\dfrac{1}{2} \sqrt{\left\vert\overrightarrow{\mathstrut a}... ...row{\mathstrut c}\cdot\overrightarrow{\mathstrut a}\right)^2}$$

となるが, $\maru{1}$を適用すると

$$\left\vert\overrightarrow{\mathstrut a}\right\vert^2\left\v... ...ht\vert^2\left\vert\overrightarrow{\mathstrut a}\right\vert^2$$

$$∴\quad \left\vert\overrightarrow{\mathstrut a}\right\ver... ...ght\vert= \left\vert\overrightarrow{\mathstrut c}\right\vert$$

すなわち

$${\rm OA}={\rm OB}={\rm OC}$$

条件(i)は３組の対辺が互いに直交することなので， 4点 $\mathrm{O},\ \mathrm{A},\ \mathrm{B},\ \mathrm{C}$に関して対称である． したがって$\mathrm{O}$の代わりに$\mathrm{A}$や$\mathrm{B}$を始点にとることで，

$$\begin{eqnarray*} &&{\rm AB}={\rm AC}={\rm AO}\\ &&{\rm BC}={\rm BO}={\rm BA} \end{eqnarray*}$$

を得る．つまり

$${\rm OA}={\rm OB}={\rm OC}={\rm AB}={\rm BC}={\rm CA}$$

したがって, 四面体OABCは正四面体である. □

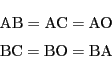
ただ，それぞれの条件自体が意味のあることのように思われるので， 各条件の意味することとその関係を考えています．

南海　 なるほど．この問題を解くだけにせず， 各条件はそれぞれどんな四面体になっているのかを考えることは大変いいことだし，必要なことだ．

条件(i)を満たす四面体を直辺四面体， 条件(ii)を満たす四面体を等積四面体と呼ぼう．それぞれの性質を詳しく調べよう． そのためには，三角形と四面体の共通点と違う点を理解しなければならない．