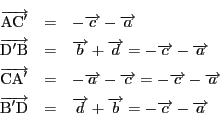次: 四面体の外心と内心 上: 特別な四面体 前: ある入試問題

四面体の重心と平行六面体への埋め込み

南海　 三角形には「五心」と呼ばれる五種類の点がある．

拓生　 重心，外心，内心，垂心，傍心 の五種です．

南海　 そのうち，一般の四面体$\mathrm{ABCD}$にもあるのは．まず重心はどうか．

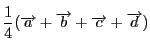拓生　 4頂点の位置ベクトルを $\overrightarrow{a},\ \overrightarrow{b},\ \overrightarrow{c},\ \overrightarrow{d}$として すぐに表せるのは重心 $\dfrac{1}{4}(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}+\overrightarrow{d})$ だけです．

南海　 重心は，正確には物理学の重心であることを示さなければならないが， そのためにはモーメントの考え方が必要だ．それは数学のなかではできない．数学的にいえば，重心は頂点の位置ベクトルの平均として定まる点だ．

頂点$\mathrm{A}$と対面の三角形の重心を$3:1$に内分する点は

$$\dfrac{3}{4}\left\{\dfrac{1}{3}(\overrightarrow{b}+\overrig... ...{a}+\overrightarrow{b}+\overrightarrow{c}+\overrightarrow{d})$$

となる． これは4つの頂点に関して対称な形なので，他の頂点と対面の重心を結ぶ線分を同じ比率で内分する点も， この点になる．つまり， 頂点と対面の重心を結ぶ4本の線分はこの1点で交わる．これが重心だ． または，四面体では，相対する辺の中点を結ぶ線分は1点で交わる，その交点が重心である，と定義してもよい．

拓生　 $\mathrm{AB}$の中点と$\mathrm{CD}$の中点を結ぶ線分の中点の位置ベクトルは

$$\dfrac{\dfrac{\overrightarrow{a}+\overrightarrow{b}}{2} +\... ...{a}+\overrightarrow{b}+\overrightarrow{c}+\overrightarrow{d})$$

となり，これは $\mathrm{A},\ \mathrm{B},\ \mathrm{C},\ \mathrm{D}$で対称なので その他についても同様で，相対する辺の中点を結ぶ線分の中点が重心に一致する．

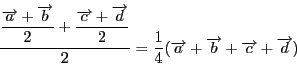
南海　 ここで四面体$\mathrm{ABCD}$で，各頂点 $\mathrm{A},\ \mathrm{B},\ \mathrm{C},\ \mathrm{D}$ と，それらの重心に関する対称点を $\mathrm{A'},\ \mathrm{B'},\ \mathrm{C'},\ \mathrm{D'}$とする． これら8点でできる図形はどのようなものか．

拓生　 基準点を重心にとり，4頂点 $\mathrm{A},\ \mathrm{B},\ \mathrm{C},\ \mathrm{D}$の位置ベクトルを $\overrightarrow{a},\ \overrightarrow{b},\ \overrightarrow{c},\ \overrightarrow{d}$とすると，

$$\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}+\overrightarrow{d}=0$$

で， $\mathrm{A'},\ \mathrm{B'},\ \mathrm{C'},\ \mathrm{D'}$の位置ベクトルは $-\overrightarrow{a},\ -\overrightarrow{b},\ -\overrightarrow{c},\ -\overrightarrow{d}$となる．

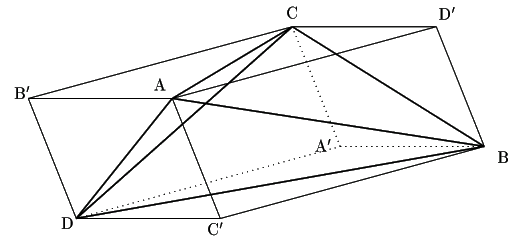
平行六面体らしいので確認してみます．

$$\begin{eqnarray*} \overrightarrow{\mathrm{AC'}}&=&-\overrightarrow{c}-\overrigh... ...ow{d}+\overrightarrow{b}=-\overrightarrow{c}-\overrightarrow{a} \end{eqnarray*}$$

つまり

$$\overrightarrow{\mathrm{AC'}}=\overrightarrow{\mathrm{D'B}}= \overrightarrow{\mathrm{CA'}}=\overrightarrow{\mathrm{B'D}}$$

他も同様なので確かに平行六面体に埋め込まれています． 四面体は重心を中心とする平行六面体に埋め込まれるのですね．