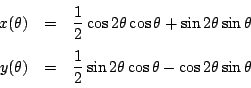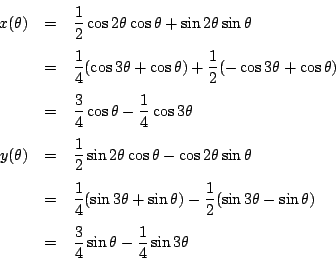次: 外サイクロイドと内サイクロイド
上: 光線の包絡線
前: 問題の設定
 南海
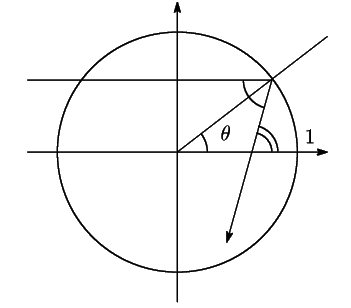
そこで,コップを原点を中心とする半径1の円としよう.
南海
そこで,コップを原点を中心とする半径1の円としよう.
図のように,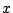 軸に平行な光線が,点
軸に平行な光線が,点
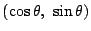 で
反射しているとしよう.
反射光の通過する直線の方程式はどのようになるか.
で
反射しているとしよう.
反射光の通過する直線の方程式はどのようになるか.
耕一
傾きは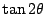 ですから
ですから
です.分母を払って整理すると
となります.これは
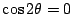 のときも成立します.
のときも成立します.
ここからは包絡線の一般論ですね.
少し難しいです.
南海
まず,何らかの曲線が存在していることは事実である.
われわれは,その曲線とこの光線が接していると考えているので,
接点を
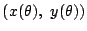 とおこう.
とおこう.
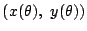 の軌跡が,この曲線そのものだ.
の軌跡が,この曲線そのものだ.
耕一
曲線がどのような媒介変数表示になるかはわからないので,
とりあえずそれを
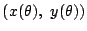 とおいたのですね.
するとこの点は光線上の点でもあるから方程式
とおいたのですね.
するとこの点は光線上の点でもあるから方程式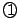 を満たし.
を満たし.
となる.
『数学対話』−「座標幾何のひろがり」−「包絡線」によれば
これを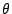 で微分するのですね.
すると
で微分するのですね.
すると
となります.
ところがベクトル
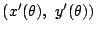 は曲線の接線方向ですから,
接線の法線ベクトル
は曲線の接線方向ですから,
接線の法線ベクトル
と直交しています,つまり
です.これを微分した式に代入して両辺を2で割ると
となります.
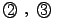 を連立して
を連立して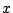 と
と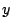 について解くと
について解くと
です.
南海
もう一息,これを積和の公式で分けるとどうなるか.
耕一
これはどこかで見たことがあります.
Aozora Gakuen
 南海
そこで,コップを原点を中心とする半径1の円としよう.
南海
そこで,コップを原点を中心とする半径1の円としよう.
![]() ですから
ですから
![]() とおこう.
とおこう.
![]() の軌跡が,この曲線そのものだ.
の軌跡が,この曲線そのものだ.
![]() とおいたのですね.
するとこの点は光線上の点でもあるから方程式
とおいたのですね.
するとこの点は光線上の点でもあるから方程式![]() を満たし.
を満たし.