 南海
それを考えるためには,ここまで考えたことを一般化しなければならない.
南海
それを考えるためには,ここまで考えたことを一般化しなければならない.
 南海
それを考えるためには,ここまで考えたことを一般化しなければならない.
南海
それを考えるためには,ここまで考えたことを一般化しなければならない.
光線が半径1の円の内側で反射してできる光線の包絡線が半径![]() の円の周りを半径
の円の周りを半径![]() がまわってできる外サイクロイドになるということだった.
がまわってできる外サイクロイドになるということだった.
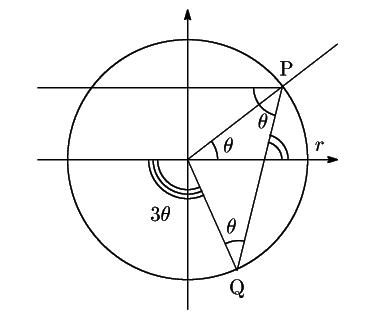
図のように半径1の円周上の点![]() で反射した光線が,
もういちど同じ円にあたる点を
で反射した光線が,
もういちど同じ円にあたる点を![]() としよう.
そして,
必ずしも反射光線の軌跡ではない一般の円の弦
としよう.
そして,
必ずしも反射光線の軌跡ではない一般の円の弦![]() の包絡線を考える.
の包絡線を考える.
その設定の仕方を,反射光線の場合から考えよう.
角![]() は同様にとるとすると,
は同様にとるとすると,
![]() が
が![]() 軸の正の方向となす角はいくらになるか.
軸の正の方向となす角はいくらになるか.
耕一
図から考えてそれは![]() です.
です.
 そうか.点
そうか.点![]() が角
が角![]() の位置にあるとき,点
の位置にあるとき,点![]() が
が
![]() の位置にあるような関係を保って弦
の位置にあるような関係を保って弦![]() が動くとき,その包絡線が2円の半径の比が2:1であるような外サイクロイドになるのだ.
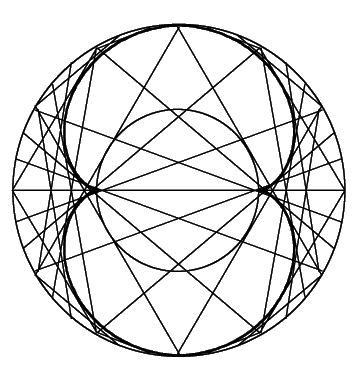
このように考えると,光が右側から当たった場合も含めて,外サイクロイドが得られるのです.
が動くとき,その包絡線が2円の半径の比が2:1であるような外サイクロイドになるのだ.
このように考えると,光が右側から当たった場合も含めて,外サイクロイドが得られるのです.
![]() ずつで
ずつで![]() を動かして書いてみました.
を動かして書いてみました.
南海 このようにいちどは手を動かして書くことは大切だ.
耕一
ところで,一般化ですが,この3を![]() にするのですか.
にするのですか.
南海
そうだ.
明らかに![]() のときは包絡線を作らないので,
のときは包絡線を作らないので,
![]() とする.
点
とする.
点![]() が角
が角![]() の位置にあるとき,
点
の位置にあるとき,
点![]() が角
が角![]() の位置にあるとして,
直線
の位置にあるとして,
直線![]() の包絡線を考えようということだ.
の包絡線を考えようということだ.
ただし点
![]() が一致するときは
直線
が一致するときは
直線![]() の包絡線を考えるときには除外しておく.
除外した
の包絡線を考えるときには除外しておく.
除外した![]() の値以外のところで得られた包絡線が
除外した
の値以外のところで得られた包絡線が
除外した![]() の値以外のところでは連続しているなら,
除外した
の値以外のところでは連続しているなら,
除外した![]() の値に対応する点も連続性によって包絡線の
点として定義される.
の値に対応する点も連続性によって包絡線の
点として定義される.
耕一
点
![]() が一致するのは,
が一致するのは,
南海
特異な点を除外して考え,後でその点を個別に考えるのがよい.
そこでこの前提で,直線![]() の方程式を求めよう.
の方程式を求めよう.
耕一
![]() ,
,
![]() ですから直線
ですから直線![]() の方程式は,
の方程式は,
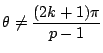 つまり
つまり
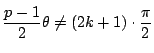 なので
なので
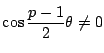 .
したがって
.
したがって
次に包絡線と直線![]() の接点を
の接点を
![]() とします.
この点は
とします.
この点は![]() 上にあるので
上にあるので
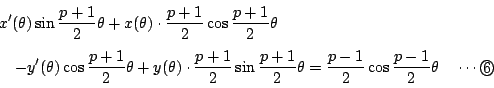
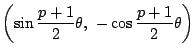 とは直交します.つまり
とは直交します.つまり
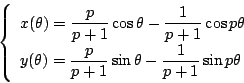
南海 これで先の質問が解けるのではないか.
耕一
![]() の表示と今得られた表示と見比べ
の表示と今得られた表示と見比べ
南海 そういうことなのだ.
耕一 逆にまた,得られた包絡線がサイクロイドであることもわかります.