上: 光線の包絡線 前: 一般化の試み

円族の包絡線としてのサイクロイド

南海　 正数$a$と正数$b$の外サイクロイドと 正数$a$と負数$-b$の内サイクロイドの相互関係を調べよう． それぞれのサイクロイド上の点を$\mathrm{P}$，$\mathrm{P}'$とすると，その媒介変数表示は

$$\begin{array}{l} \overrightarrow{\mathrm{OP}} =(a+b)\veca... ...right)} {\sin\left(\dfrac{a-b}{-b}\theta \right)} \end{array}$$

となる．また点$\mathrm{T}$を $\mathrm{T}(a\cos\theta,\ a\sin\theta)$とする．

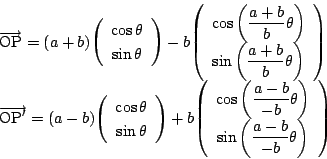
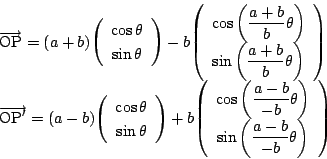
耕一　 この場合同じ半径$b$の動円が半径$a$の基準円の内と外をまわるので， 点$\mathrm{P}$と点$\mathrm{P}'$は同時に基準円に戻ります．

南海　 そう，その上で ベクトル $\overrightarrow{\mathrm{TP}}$と点$\mathrm{P}$でのサイクロイドの接線は直交している． これを確認してほしい．

耕一　 $\mathrm{P}(x(\theta),\ y(\theta))$とします． まず

$$\overrightarrow{\mathrm{TP}}=b\vecarray{\cos\theta}{\sin\the... ... \right)} {\sin\theta-\sin\left(\dfrac{a+b}{b}\theta \right)}$$

です．一方

$$\vecarray{x'(\theta)}{y'(\theta)} =(a+b)\vecarray{-\sin\thet... ... \right)} {\cos\theta-\cos\left(\dfrac{a+b}{b}\theta \right)}$$

なので，これから

$$\overrightarrow{\mathrm{TP}}\cdot\vecarray{x'(\theta)}{y'(\theta)} =0$$

となります．

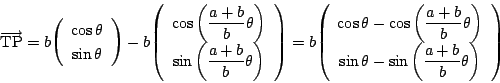
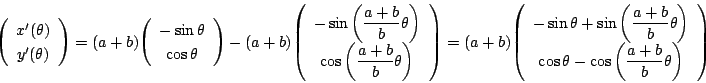
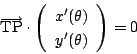
南海　 同様に ベクトル $\overrightarrow{\mathrm{TP}'}$と点$\mathrm{P}'$でのサイクロイドの接線も直交している． また，

$$\overrightarrow{\mathrm{TP}'} =-b\vecarray{\cos\theta-\cos\l... ...\right)} {\sin\theta-\sin\left(\dfrac{a-b}{-b}\theta \right)}$$

なので

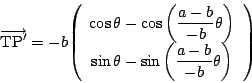
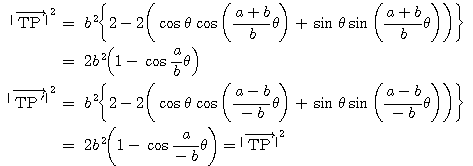
以上のことから，2つのサイクロイドは， 点$\mathrm{T}$を中心とする 半径 $\left\vert\overrightarrow{\mathrm{TP}} \right\vert$の円に接していることがわかる．

いいかえると，基準円上に中心をもち外サイクロイドに接する円の集合(円族)の通過領域の境界は， 動円の半径が等しい内サイクロイドになる．内外逆にしても成立する．

耕一　すると，このような外サイクロイドに接するということで定まる円の群が，内サイクロイドに接している．ということは包絡線と似ています．

南海　そうだ．媒介変数 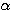をもつ曲線族  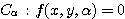がある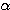． が連続的に変化するとき，曲線族  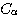が常にある曲線 Eに接し，しかも E がその接点の軌跡であるとき， E を曲線族 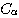 の 包絡線 という．今の場合

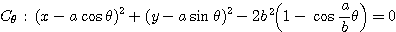
とするとこの曲線族が内サイクロイドを包絡線にもつということだ．

耕一　 いくつか例を書いてみます．

$a=1$で $b=\dfrac{1}{2}$のとき．内サイクロイドは退化した直径です． $a=1$で $b=\dfrac{1}{3}$のとき．そ相互関係の方を描いてみました．

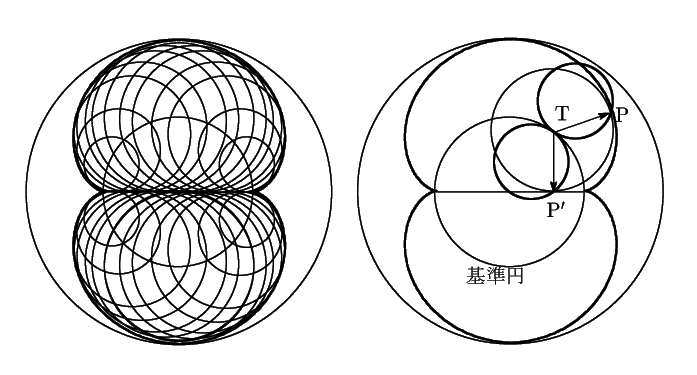
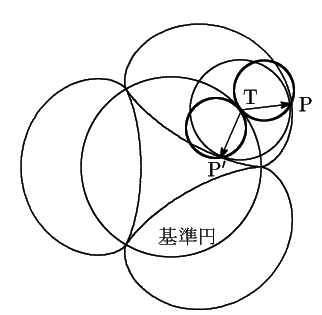
南海　この対話では，『初等数学』を発行しておられる松田康雄さんによる「円サイクロイド」（『日本数学協会論文集』第4号2008年所収）を参考にした．感謝します．