次： 面積速度一定の法則 上： 運動方程式を読み解く 前： 運動程式を読み解く

惑星運動は平面運動である

拓生　 いま考えているベクトルは空間ベクトルですか．

南海　 そうだ．しかし次のことを示せば，あとは平面ベクトルだけを考えればよい． ここで中心力とは，2つの質点の間で2つの質点を結ぶ直線方向に働く力のことである．

定理 1
太陽と地球の間に中心力のみが働いている場合， 地球は，一つの平面上を運動する．

拓生　 つまり

$$m\dfrac{d^2}{dt^2}\overrightarrow{r} =f(r)\dfrac{-\overrightarrow{r}}{\vert\overrightarrow{r}\vert} \quad \cdots\maru{2}$$

とかける場合ですね．

考えれば他に力が働かないのだから， 太陽と地球を結ぶ直線と，ある時刻における速度ベクトルとで定まる平面を離れようがない．

南海　 そういうことだが，これを数学的に示すことが出来る．

外積の定義

南海　 力学の諸法則を書きあらわす言葉として外積が有用である． 今後も役に立つので，ベクトルの外積を定義しよう． これは数学の範囲のことである．

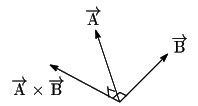
2つのベクトル $\overrightarrow{\mathrm{A}}$と $\overrightarrow{\mathrm{B}}$がある． ベクトル $\overrightarrow{\mathrm{A}}$からベクトル $\overrightarrow{\mathrm{B}}$へ右ネジを回転させたとき， ネジの進む方向の単位ベクトルを $\overrightarrow{k}$とおく． また $\overrightarrow{\mathrm{A}}$と $\overrightarrow{\mathrm{B}}$のなす角を$\theta$とおく．

このときベクトル $\overrightarrow{\mathrm{A}}$と $\overrightarrow{\mathrm{B}}$の外積を次式で定める．

$$\overrightarrow{\mathrm{A}}\times\overrightarrow{\mathrm{B}}... ...overrightarrow{\mathrm{B}}\vert \sin \theta \overrightarrow{k}$$

拓生　 内積の時と同様に， $\overrightarrow{\mathrm{A}}=(x_1,\ y_1,\ z_1)$と $\overrightarrow{\mathrm{B}}=(x_2,\ y_2,\ z_2)$に対して $\overrightarrow{\mathrm{A}}\times\overrightarrow{\mathrm{B}}$ を成分で表さなければならない．

大きさは

です．しかし方向はどのようにとればよいのか．

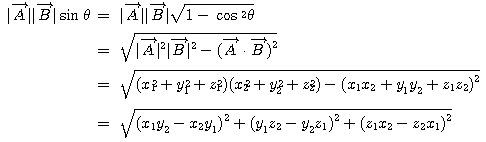
南海　 結論的にいうと

$$\overrightarrow{\mathrm{A}}\times\overrightarrow{\mathrm{B}}= (y_1z_2-y_2z_1,\ z_1x_2-z_2x_1,\ x_1y_2-x_2y_1)$$

とすればよい．

拓生　

$$(\overrightarrow{\mathrm{A}}\times\overrightarrow{\mathrm{B}... ...} =(y_1z_2-y_2z_1)x_1+(z_1x_2-z_2x_1)y_1+(x_1y_2-x_2y_1)z_1 =0$$

ですから $\overrightarrow{\mathrm{A}}\times\overrightarrow{\mathrm{B}}\bot \overrightarrow{\mathrm{A}}$，同様に $\overrightarrow{\mathrm{A}}\times\overrightarrow{\mathrm{B}}\bot \overrightarrow{\mathrm{B}}$も成り立ちます．

でも，右ネジの進む方向というのはどのように示せばよいのかわかりません．

南海　 後は方向だけなので，ベクトル全体を回転し，

$$\begin{eqnarray*} \overrightarrow{\mathrm{A}}&=&(a,\ 0,\ 0)\ (a>0)\\ \overright... ...}&=&(b\cos \theta,\ b\sin \theta,\ 0) \quad (b>0,\ 0<\theta<\pi) \end{eqnarray*}$$

としてみる．外積は

となり， 確かに $\overrightarrow{\mathrm{A}}$から $\overrightarrow{\mathrm{B}}$へ右ネジを回したときの進む方向になっている．

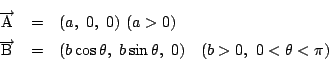
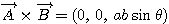
したがって外積は次のような計算法則を満たす．

$$\begin{eqnarray*} \overrightarrow{\mathrm{A}}\times\overrightarrow{\mathrm{B}}&=... ...}} +\overrightarrow{\mathrm{A}}\times\overrightarrow{\mathrm{C}} \end{eqnarray*}$$

外積と微分

南海　 $\overrightarrow{\mathrm{A}}=(x_1,\ y_1,\ z_1)$と $\overrightarrow{\mathrm{B}}=(x_2,\ y_2,\ z_2)$の各成分が$t$の関数のとき，

$$\dfrac{d}{dt}(\overrightarrow{\mathrm{A}}\times\overrightarr... ...dfrac{d}{dt}(y_1z_2-y_2z_1,\ z_1x_2-z_2x_1,\ x_1y_2-x_2y_1)\\$$

を考えると，$x$成分についてみれば

$$\begin{eqnarray*} \dfrac{d}{dt}(y_1z_2-y_2z_1) &=&\dfrac{dy_1}{dt}z_2+y_1\dfrac{... ...z_1\right)+ \left(y_1\dfrac{dz_2}{dt}-y_2\dfrac{dz_1}{dt}\right) \end{eqnarray*}$$

となる．他の成分についても同様なので，

$$\dfrac{d}{dt}(\overrightarrow{\mathrm{A}}\times\overrightarr... ...A}}\times\left(\dfrac{d}{dt}\overrightarrow{\mathrm{B}}\right)$$

が成り立つ．

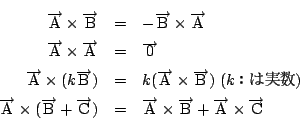
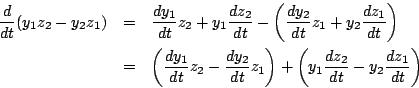
拓生　 内積でも，行列の積でも，積のそれぞれの成分がもとの成分の積の和や差で作られているときは， 同様の微分公式が成り立ちます．

外積はどんなところで用いられるのですか．

角運動量

南海　 外積を用いて記述される一番基本的な物理量は力のモーメントだ．

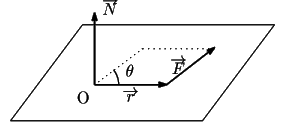図のように， 力 $\overrightarrow{F}$が位置ベクトル $\overrightarrow{r}$の質点$\mathrm{P}$に作用するとき， ベクトル $\overrightarrow{N}=\overrightarrow{r}\times\overrightarrow{F}$を 力 $\overrightarrow{F}$の基準点$\mathrm{O}$の周りにもつモーメントという．

拓生　 $\overrightarrow{r}$と $\overrightarrow{F}$のなす角を$\theta$とすると， ベクトル $\overrightarrow{N}$の大きさは $\vert\overrightarrow{r}\vert\cdot\vert\overrightarrow{F}\vert\sin\theta$ です． $\vert\overrightarrow{F}\vert\sin\theta$はちょうど力 $\overrightarrow{F}$の $\overrightarrow{r}$と直交する方向の大きさになるので， 力のモーメントの大きさは点$\mathrm{O}$の周りの回転させる力の強さのようです．

南海　 そうだ．モーメントは力に関するものだけではない．

一般に， 質点$\mathrm{P}$にある物理量 $\overrightarrow{G}$と 基準点$\mathrm{O}$に関する$\mathrm{P}$の位置ベクトル $\overrightarrow{r}$に対して， 外積 $\overrightarrow{r}\times\overrightarrow{G}$を $\overrightarrow{G}$が点$\mathrm{O}$の周りにもつモーメントという．

$\overrightarrow{G}$が運動量

$$\overrightarrow{p}=m\overrightarrow{v}=m\dfrac{d}{dt}\overrightarrow{r}$$

であるとき，この運動量 $\overrightarrow{p}$のモーメントを角運動量という．

角運動量保存則の証明

南海　 ニュートンの第3法則，つまり作用反作用の法則が成り立つ質点では，外力が作用しないかぎり， 角運動量は時間に対して変化しない． これはまず当然であるが，外力が作用してもその作用線がつねに固定点を通るとき， このときも，その点の周りの角運動量は一定である．

これを証明しよう．この事実が，惑星運動は平面上の運動であることを意味する．

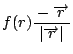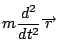固定点を基準点に取る． 質点に作用する力は $f(r)\dfrac{-\overrightarrow{r}}{\vert\overrightarrow{r}\vert}$と表される． ニュートンの第2法則から， この力が $m\dfrac{d^2}{dt^2}\overrightarrow{r}$と釣り合っている．つまり運動方程式

$$m\dfrac{d^2}{dt^2}\overrightarrow{r} =f(r)\dfrac{-\overrightarrow{r}}{\vert\overrightarrow{r}\vert}$$

が成り立つ，

両辺のモーメントをとる．左から $\overrightarrow{r}$を外積でかける．

$$\overrightarrow{r}\times\left(m\dfrac{d^2}{dt^2}\overrightar... ...rrightarrow{r}\vert}\overrightarrow{r}\times\overrightarrow{r}$$

拓生 右辺は $\overrightarrow{r}\times\overrightarrow{r}=\overrightarrow{0}$より， $\overrightarrow{0}$です．

南海　 一方，

$$\begin{eqnarray*} &&\dfrac{d}{dt}\left(\overrightarrow{r}\times \dfrac{d}{dt}\ov... ... &=&\overrightarrow{r}\times\dfrac{d^2}{dt^2}\overrightarrow{r} \end{eqnarray*}$$

である．したがって

$$\dfrac{d}{dt}\left(\overrightarrow{r}\times \dfrac{d}{dt}\overrightarrow{r}\right) =\overrightarrow{0}$$

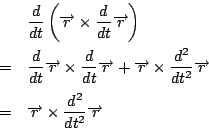
拓生　 そうか．つまり，

$$\overrightarrow{r}\times \dfrac{d}{dt}\overrightarrow{r}=\overrightarrow{c}\ (定ベクトル)$$

が成り立つ．

運動量ベクトルは 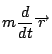$m\dfrac{d}{dt}\overrightarrow{r}$なので これはまさに角運動量が時間に対して一定であることを示している．

一方， これは2つのベクトル $\overrightarrow{r}$と $\dfrac{d}{dt}\overrightarrow{r}$がつねに $\overrightarrow{c}$と直交していることを示す．

運動は時間に関して連続的であるから， 2つのベクトル $\overrightarrow{r}$と $\dfrac{d}{dt}\overrightarrow{r}$が つねに同一の平面上にあることが示された．

そういうことですね．

次： 面積速度一定の法則 上： 運動程式を読み解く 前： 運動程式を読み解く